
����Ŀ����ͼ,���ı���ABCD��,AD��BC, ��B��90��,AB��8�M,AD��24�M,BC��26�M,��p�ӵ�A����,��1�M/s���ٶ����D�˶�;��Q�ӵ�Cͬʱ����,��3�M/s���ٶ����B�˶�,�涨����һ�����㵽��˵�ʱ,��һ������Ҳ��ֹ֮ͣ�˶�. ���˶�ʱ��Ϊt s.
��1��tΪ��ֵʱ,�ı���PQCDΪƽ���ı���?
��2��tΪ��ֵʱ,�ı���PQCDΪ��������?���������ε�������ȣ�������ȣ�
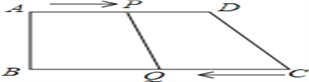
���𰸡���1����t=6ʱ���ı���PQCD��ƽ���ı��Σ���2������7s�ı���PQCD�ǵ������Σ�
���������������: ��1����������ɵ�PA=t��CQ=3t����PD=AD-PA=24-t����PD=CQʱ���ı���PQCDΪƽ���ı��Σ��ɵ÷���24-t=3t����˷��̼�����ô𰸣�
��2������D��DE��BC����CE=BC-AD=2cm��CQ-PD=4ʱ���ı���PQCD�ǵ������Σ���3t-��24-t��=4�����t��ֵ���ɣ�
�������:
��1���˶�ʱ��Ϊt s.
AP= t ,PD=24-t��CQ=3t��
����ts�ı���PQCDƽ���ı���
��ʱ��PD=CQ
��24-t=3t
���t=6��
��t=6ʱ���ı���PQCD��ƽ���ı��Σ�
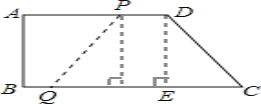
��2����ͼ������D��DE��BC��
��CE=BC-AD=2cm��
��CQ-PD=4ʱ���ı���PQCD�ǵ������Σ�
��3t-��24-t��=4
��t=7��
�ྭ��7s�ı���PQCD�ǵ������Σ�
�㾦: ������Ҫ������ƽ���ı��Ρ��������ε��ж�������Ӧ�ã�Ҫ��ѧ�����նԸ���ͼ�ε���ʶ��ͬʱѧ�����ν�ϵ���ѧ����˼�룮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���߳�Ϊ4cm���������۵�Χ��һ���������IJ��棬�����������ĵ�����һ�������Σ���������α߳�Ϊ_______cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
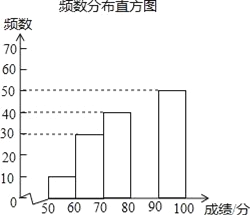
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣬Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵġ�������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ����ɼ�xȡ�������ܷ�100�֣���Ϊ���������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.05 |
��60��x��70 | 30 | 0.15 |
��70��x��80 | 40 | n |
��80��x��90 | m | 0.35 |
��90��x��100 | 50 | 0.25 |
�����������Ϣ������������⣺
��1��m=�� ����n=�� ����
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����α����ɼ�����λ���������� �������Σ�
��4�����ɼ���90�����ϣ�����90�֣���Ϊ���š��ȣ����У�μ���α�����3000��ѧ���гɼ����š���Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͬ���ڽǻ�������ֱ��ƽ����д�������������ô����������ʽ��___________________����_______����(����������������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ρ����Ρ������ζ�һ�����е������ǣ�������
A. �ڱ���� B. �ĸ��Ƕ���ֱ��
C. �Խ������ D. �Խ�����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������A��B��C���㣬�ֱ��ʾ����24����10��10����ֻ�������ϼס��ҷֱ��A��C����ͬʱ������У����ٶ�Ϊ4����λ/�룬�ҵ��ٶ�Ϊ6����λ/�룮
��1���ʼס����������ϵ��ĸ���������
��2���ʶ�������A��B��C����ľ���֮��Ϊ40����λ����
��3�����ס�����ֻ�������ϣ���P��ʾ�����ϡ�Q��ʾ�����ϣ��ֱ��A��C����ͬʱ������У����ٶȱ�Ϊԭ����3�����ҵ��ٶȲ��䣬ֱ��д������ʱ���ԭ��O��������P��������Q�����У���һ��ǡ���������������߶ε��е㣮
![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com