
分析 (1)利用不等式的性质求得解集即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)1-$\frac{x+3}{5}$≥x-$\frac{x-1}{3}$
15-3(x+3)≥15x-5(x-1)
15-3x-9≥15x-5x+5
-3x-15x+5x≥5+9-15
-13x≥-1
x≤$\frac{1}{13}$
(2)$\left\{\begin{array}{l}{4x+6<3x+7①}\\{3x+14>4(2x-9)②}\end{array}\right.$,
由①得,x<1;
由②得,x<10,
故此不等式组的解集为:x<1.
点评 本题考查的是解一元一次不等式组与不等式,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 已知:抛物线经过A(2,0)、B(8,0)、C(0,$\frac{16\sqrt{3}}{3}$);设抛物线的顶点为P,把△APB翻折,使点P落在线段AB上(不与A、B重合),记作P′,折痕为EF.
已知:抛物线经过A(2,0)、B(8,0)、C(0,$\frac{16\sqrt{3}}{3}$);设抛物线的顶点为P,把△APB翻折,使点P落在线段AB上(不与A、B重合),记作P′,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 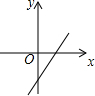 | C. | 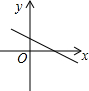 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
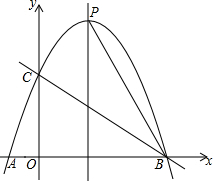 如图,抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于M,连接PB.
如图,抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于M,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
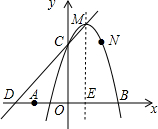 如图,已知抛物线y=-x2+2x+3的顶点为M,且经过点N(2.3),与x轴交于两点(点A在点B左侧),与y轴交于点C.
如图,已知抛物线y=-x2+2x+3的顶点为M,且经过点N(2.3),与x轴交于两点(点A在点B左侧),与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com