
【题目】阅读下面“将无限循环小数化为分数”材料,并解决相应问题:
我们知道分数![]() 写为小数形式即为
写为小数形式即为![]() ,反之,无限循环小数
,反之,无限循环小数![]() 写成分数形式即
写成分数形式即![]() .一般地,任何一个无限循环小数都可以写成分数形式吗?如果可以,应怎样写呢?
.一般地,任何一个无限循环小数都可以写成分数形式吗?如果可以,应怎样写呢?
(发现)先以无限循环小数![]() 为例进行讨论.
为例进行讨论.
设![]() =x,由
=x,由![]() =0.777…可知,10x=7.777…,即10x﹣x=7.解方程,得x=
=0.777…可知,10x=7.777…,即10x﹣x=7.解方程,得x=![]() .于是
.于是![]() =
=![]() ,
,
(类比探究)再以无限循环小数![]() 为例,做进一步的讨论.
为例,做进一步的讨论.
无限循环小数![]() =0.737373…,它的循环节有两位,类比上面的讨论可以想到如下做法.
=0.737373…,它的循环节有两位,类比上面的讨论可以想到如下做法.
设![]() =x,由
=x,由![]() =0.737373…可知,100x=73.7373…,所以100x﹣x=73.解方程,得x=
=0.737373…可知,100x=73.7373…,所以100x﹣x=73.解方程,得x=![]() ,于是得
,于是得![]() =
=![]()
(解决问题)
(1)请你把无限小数![]() 写成分数形式,即
写成分数形式,即![]() = ;
= ;
(2)请你把无限小数![]() 写成分数形式,即
写成分数形式,即![]() = ;
= ;
(3)根据以上过程比较![]() 与1的大小关系,并说明你的理由.
与1的大小关系,并说明你的理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() =1.理由见解析.
=1.理由见解析.
【解析】
(1)根据题意设![]() =x,由
=x,由![]() =0.444…可知,10x-x的值,进而求出即可;
=0.444…可知,10x-x的值,进而求出即可;
(2)根据题意设![]() =x,由
=x,由![]() =0.7575…可知,100x-x的值,进而求出即可;
=0.7575…可知,100x-x的值,进而求出即可;
(3)根据题意设![]() =x,由
=x,由![]() =0.999…可知,10x-x的值,进而求出即可.
=0.999…可知,10x-x的值,进而求出即可.
(1)设![]() =x,由
=x,由![]() =0.444…可知,10x﹣x=
=0.444…可知,10x﹣x=![]() ﹣
﹣![]() =4,
=4,
即10x﹣x=4.
解得x=![]() .
.
于是,得![]() =
=![]() ;
;
(2)设![]() =x,由
=x,由![]() =0.7575…可知,100x﹣x=75.
=0.7575…可知,100x﹣x=75.
![]() ﹣
﹣![]() =75,
=75,
即100x﹣x=75.
解得x=![]() .
.
于是,得![]() =
=![]() ;
;
(3)设![]() =x,由
=x,由![]() =0.999…可知,10x﹣x=
=0.999…可知,10x﹣x=![]() ﹣
﹣![]() =9,
=9,
即10x﹣x=9.
解得x=1.
于是,得![]() =1.
=1.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中(如图),已知抛物线y=﹣x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
(1)求这条抛物线的表达式和点B的坐标;
(2)点M在对称轴上,且位于顶点上方,设它的纵坐标为m,联结AM,用含m的代数式表示∠AMB的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点C在x轴上.原抛物线上一点P平移后的对应点为点Q,如果OP=OQ,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打笫一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() .点Р从点B出发沿折线段
.点Р从点B出发沿折线段![]() 以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段
以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点O向上作射线OKIBC,交折线段![]()
![]() 于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒
于点E.点P、O同时开始运动,为点Р与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒![]() .
.
(1)点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点Р运动到AD上时,t为何值能使![]() ?
?
(3)t为何值时,四点P、Q、C、E成为一个平行四边形的顶点?
(4)![]() 能为直角三角形时t的取值范围________.(直接写出结果)
能为直角三角形时t的取值范围________.(直接写出结果)
(注:备用图不够用可以另外画)




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正.减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增减 | +5 | -2 | -5 | +9 | -10 | +16 | -9 |
(1)根据记录的数据可知该厂星期四生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(4)该厂实行每周计件工资制,每生产一辆车可得100元,若超额完成任务,则超过部分每辆另奖30元;少生产一辆扣40元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸是一名出租车司机,一天下午小明的爸爸以某超市为出发点,在东西方向的公路上运营,记向东为正,向西为负,以先后次序记录如下:(单位km)
+5,﹣3,﹣5,+4,﹣8,+6,﹣4
(1)将最后一名乘客送到目的地时,出租车离出发点有多远?在它的什么方向?
(2)若每千米收费为2元,小明爸爸这个下午的营业额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
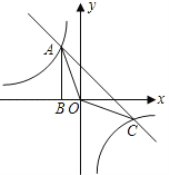
【题目】如图,Rt△ABO的顶点A是双曲线y1=![]() 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 和三角形
和三角形![]() 在同一平面内.
在同一平面内.

(1)如图1,点![]() 在
在![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .若
.若![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() ,证明:
,证明:![]() .
.
(3)点![]() 是三角形
是三角形![]() 外部的任意一点,过
外部的任意一点,过![]() 作
作![]() 交直线
交直线![]() 于
于![]() ,
,![]() 交直线
交直线![]() 于
于![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系(不需证明).
的数量关系(不需证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com