
分析 先由平均数的公式计算出x的值,再根据方差的公式计算.一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].
解答 解:x=1×6-1-2-0-(-1)-1=3,
s2=$\frac{1}{6}$[(1-1)2+(2-1)2+(0-1)2+(-1-1)2+(3-1)2+(1-1)2]=$\frac{5}{3}$.
故答案为$\frac{5}{3}$.
点评 本题考查了方差的定义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


科目:初中数学 来源: 题型:填空题
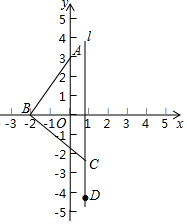 如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.
如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
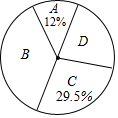 某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.
某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.| 分组 | 次数x(个) | 人数 |
| A | 0≤x<120 | 24 |
| B | 120≤x<130 | 72 |
| C | 130≤x<140 | |
| D | x≥140 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
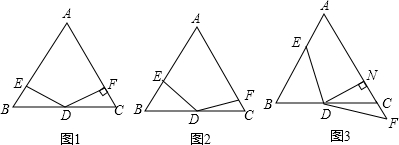
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
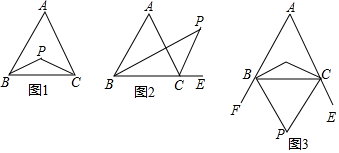
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com