
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
【答案】(1)甲![]() 万元,乙
万元,乙![]() 万元;(2)有
万元;(2)有![]() 种;(3)选购甲型设备
种;(3)选购甲型设备![]() 台,乙型设备
台,乙型设备![]() 台
台
【解析】
(1)设甲型设备每台的价格为x万元,乙型设备每台的价格为y万元,根据“购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买甲型设备m台,则购买乙型设备(10m)台,由购买甲型设备不少于3台且预算购买节省能源的新设备的资金不超过110万元,即可得出关于m的一元一次不等式组,解之即可得出各购买方案;
(3)由每月要求总产量不低于2040吨,可得出关于m的一元一次不等式,解之结合(2)的结论即可找出m的值,再利用总价=单价×数量求出两种购买方案所需费用,比较后即可得出结论.
解:(1)设甲型设备每台的价格为![]() 万元,乙型设备每台的价格为
万元,乙型设备每台的价格为![]() 万元,
万元,
根据题意得: ![]() ,
,
解得: ![]()
答:甲型设备每台的价格为![]() 万元,乙型设备每台的价格为
万元,乙型设备每台的价格为![]() 万元.
万元.
(2)设购买甲型设备![]() 台,则购买乙型设备
台,则购买乙型设备![]() 台,
台,
根据题意得: 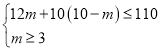
解得:![]()
∵![]() 取非负整数,∴
取非负整数,∴![]()
∴该公司有![]() 种购买方案,
种购买方案,
方案一:购买甲型设备![]() 台、乙型设备
台、乙型设备![]() 台;
台;
方案二:购买甲型设备![]() 台、乙型设备
台、乙型设备![]() 台;
台;
方案三:购买甲型设备![]() 台、乙型设备
台、乙型设备![]() 台
台
(3)由题意:![]() ,解得:
,解得:![]() ,
,
∴![]() 为
为![]() 或
或![]()
当![]() 时,购买资金为:
时,购买资金为:![]() (万元)
(万元)
当m=5时,购买资金为:![]() (万元)
(万元)
∵![]() ,
,
∴最省钱的购买方案为:选购甲型设备![]() 台,乙型设备
台,乙型设备![]() 台
台


科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,延长
中,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() .则下列说法:①
.则下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点,其中
两点,其中![]() 、
、![]() 是方程的
是方程的![]() 两根,且
两根,且![]() .
.
(![]() )求抛物线的解析式;
)求抛物线的解析式;
(![]() )直线
)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为直角三角形.若存在,求所有
为直角三角形.若存在,求所有![]() 点坐标;反之说理;
点坐标;反之说理;
(![]() )点
)点![]() 为
为![]() 轴上方的抛物线上的一个动点(
轴上方的抛物线上的一个动点(![]() 点除外),连
点除外),连![]() 、
、![]() ,若设
,若设![]() 的面积为
的面积为![]() .
. ![]() 点横坐标为
点横坐标为![]() ,则
,则![]() 在何范围内时,相应的点
在何范围内时,相应的点![]() 有且只有
有且只有![]() 个.
个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在经典朗读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干名学生进行调查,绘制出两幅不完整的统计图,请你根据图中的信息解答下列问题:

(1)被调查的学生共有 人,图2中A等级所占的圆心角为_ 度。
(2)补全折线统计图。
(3)若该校共有学生1500人,请你估计全校评价B等级学生的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AB=AC=6![]() ,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.
,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图11,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0)、A(2,1)、B(1,-2),P(a,b)是△OAB的边AB上一点.
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1 ,使它与△OAB的相似比为2:1,并分别写出点A、P的对应点A1、P1的坐标;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后的△O2A2B2 ,并写出点A、P的对应点A2、P2的坐标;
(3)判断△OA1B1与△O2A2B2 ,能否是关于某一点M为位似中心的位似图形,若是,请在图11中标出位似中心M,并写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com