
【题目】已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.
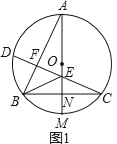
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
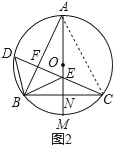
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
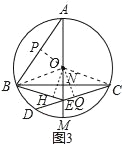
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
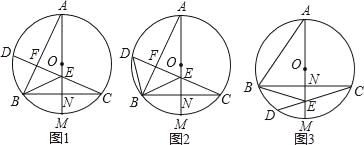
【答案】(1)见解析;(2)见解析;(3)3
【解析】
(1)根据垂径定理可得BN=CN,根据垂直平分线的性质可得EB=EC,从而可得∠BED=2∠BCD,只需证明∠BAM=∠BCD即可;
(2)连接AC,如图2,易得BC=2CN,要证AE=2CN,只需证AE=BC,只需证△ABE≌△CDB,只需证BE=BD即可;
(3)过点O作OP⊥AB于P,作OH⊥BE于H,作OQ⊥CD于Q,连接OC,如图3,由AB=CD可推出OP=OQ,易证∠BEA=∠CEA,根据角平分线的性质可得OH=OQ,即可得到OP=OH,则有![]() ,从而可得
,从而可得![]() 由AE=11可求出AO、EO,就可求出AM、EM.
由AE=11可求出AO、EO,就可求出AM、EM.
解:(1)∵BC⊥AM,CD⊥AB,
∴∠ENC=∠EFA=90°.
∵∠AEF=∠CEN,
∴∠BAM=∠BCD.
∵AM是⊙O直径,弦BC⊥AM,
∴BN=CN,
∴EB=EC,
∴∠EBC=∠BCD,
∴∠BED=2∠BCD=2∠BAM;
(2)连接AC,如图2,
∵AM是⊙O直径,弦BC⊥AM,
∴![]() =
=![]()
∴∠BAM=∠CAM,
∴∠BDC=∠BAC=2∠BAM=∠BED,
∴BD=BE.
在△ABE和△CDB中,

∴△ABE≌△CDB,
∴AE=CB.
∵BN=CN,
∴AE=CB=2CN;
(3)过点O作OP⊥AB于P,作OH⊥BE于H,作OQ⊥CD于Q,连接OC,如图3,
则有![]()
∵AB=CD,
∴AP=CQ,
∴![]()
∵AM垂直平分BC,
∴EB=EC,
∴∠BEA=∠CEA.
∵OH⊥BE,OQ⊥CD,
∴OH=OQ,
∴OP=OQ=OH,
∴
又∵![]()
∴![]()
设AO=7k,则EO=4k,
∴AE=AO+EO=11k=11,
∴k=1,
∴AO=7,EO=4,
∴AM=2AO=14,
∴EM=AM﹣AE=14﹣11=3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】食品安全是老百姓关注的话题,在食品中添加过量的添加剂对人体有害,但适量的添加剂对人体无害且有利于食品的储存和运输.某饮料加工厂生产的A、B两种饮料均需加入同种添加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产了多少瓶?

查看答案和解析>>
科目:初中数学 来源: 题型:
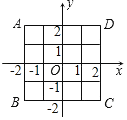
【题目】如图,在直角坐标系中的正方形ABCD边长为4,正方形ABCD的中心为原点O.现做如下实验:抛掷一枚均匀的正方体的骰子(六个面分别标有1至6这六个点数中的一个),每个面朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第次的点数作为横坐标,第二次的点数作为纵坐标)
(1)求点P落在正方形ABCD面上(含正方形内部和边界)的概率;
(2)试将正方形ABCD平移整数个单位,则是否存在一种平移,使点P落在正方形ABCD面上的概率为![]() ?若存在,请指出平移方式;若不存在,请说明理由.
?若存在,请指出平移方式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
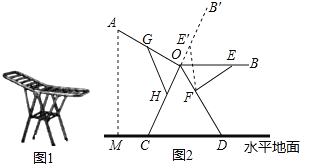
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江门旅游文化节开幕前,某茶叶公司预测今年茶叶能够畅销,就用32000元购进了一批茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批茶叶,所购数量是第一批购进数量的2倍,但每千克茶叶进价多了10元.
(1)该茶叶公司两次共购进这种茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
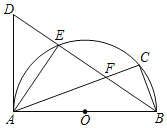
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且DE=FE.
(1)求证:AD为⊙O切线;
(2)若AB=20,tan∠EBA=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应国家有关开展中小学生“课后服务”的政策,某学校课后开设了A:课后作业辅导、B:书法、C:阅读、D:绘画、E:器乐,五门课程供学生选择;其中A(必选项目),再从B、C、D、E中选两门课程.
(1)若学生小玲第一次选一门课程,直接写出学生小玲选中项目E的概率;
(2)若学生小强和小明在选项的过程中,第一次都是选了项目E,那么他俩第二次同时选择书法或绘画的概率是多少?请用列表法或画树状图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com