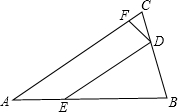
��1����x=0ʱ��y=3��
��y=0ʱ��-x+3=0�����x=3��
���B��C������ΪB��3��0����C��0��3����
�֡������߹�x���ϵ�A��B���㣬�ҶԳ���Ϊx=2��
���������ߵĶԳ��ԣ�
���A��������1��0����
��
��
���
��
�������ߵĽ���ʽΪy=x
2-4x+3��
��2����ƽ�ƺ��ֱ�߽���ʽΪy=-x+b��
��
��
��x
2-3x+3-b=0��
������������Gֻ��һ�������㣬
���=b
2-4ac=��-3��
2-4��1����3-b��=9-12+4b=0��
���b=
��
3-
=
��
������ƽ����
�����
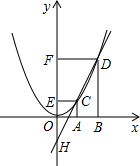
��3����A��1��0����B��3��0����

��AB=3-1=2��
�ٵ�AB�DZ�ʱ���ߵ�E�ڶԳ����ϣ�ƽ���ı��εĶԱ�ƽ������ȣ�
��EF=AB=2��
���F�ĺ�����Ϊ0��4��
��������Ϊ0ʱ��y=0
2-4��0+3=3��
��������Ϊ4ʱ��y=4
2-4��4+3=3��
���F������ΪF
1��0��3����F
2��4��3����
��ʱ��E������ΪE
1��2��3����
��ʱAE=
=
��
��ƽ���ı��ε��ܳ�Ϊ��2��AB+AE��=2��2+
��=4+2
��
�ڵ�AB��Ϊ�Խ���ʱ��EF��AB���ഹֱƽ�֣�
��y=x
2-4x+3=��x-2��
2-1��
���ʱ��E��F������ΪE
2��2��1����F
3��2��-1����
��AE=
=
��
AF=
=
��
��ƽ���ı��ε��ܳ�Ϊ��2��AE+AF��=2��
+
��=4
��
������������E��F������ֱ�ΪE
1��2��3����F
1��0��3����F
2��4��3������ʱƽ���ı��ε��ܳ�Ϊ4+2
��
��E
2��2��1����F
3��2��-1������ʱƽ���ı��ε��ܳ�Ϊ4
��
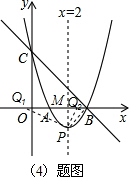
��4������PB����y=x
2-4x+3=��x-2��
2-1����P��2��-1����
�������ߵĶԳ��ύx���ڵ�M��
����Rt��PBM��PM=MB=1��
���PBM=45�㣬PB=
��
�ɵ�B��3��0����C��0��3����OB=OC=3���ڵ���ֱ��������OBC�У���ABC=45�㣬
�ɹ��ɶ�������BC=3
��
������x���ϴ��ڵ�Q��ʹ���Ե�P��B��QΪ��������������ABC���ƣ�
��PB��AB�Ƕ�Ӧ��ʱ���ߡ�PBQ=��ABC=45�㣬
��
=
��
��
=
��
���BQ=3��
�֡�BO=3��
���Q���O�غϣ�
��Q
1�������ǣ�0��0����
��PB��BC�Ƕ�Ӧ��ʱ���ߡ�PBQ=��ABC=45�㣬
��
=
��
��
=
��
���QB=
��
��OB=3��
��OQ=OB-QB=3-
=
��
��Q
2�������ǣ�
��0����
�ۡߡ�PBx=180��-45��=135�㣬��BAC��135�㣬
���PBx�١�BAC��
���Q��������B���Ҳ��x����
������������x���ϴ�������Q
1��0��0����Q
2��
��0������ʹ���Ե�P��B��QΪ��������������ABC���ƣ�







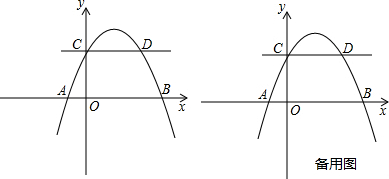


 ��x=-1������B��1��0����C��0��-3����
��x=-1������B��1��0����C��0��-3����