
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.
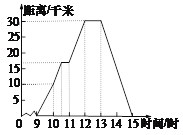
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
【答案】3小时、30千米;10点休息、半小时;返回途中、15千米/小时;10千米/小时.
【解析】试题分析:本题是一道函数图象的基础题,解题的关键是通过仔细观察图象,从中整理出解题时所需的相关信息,因此本题实际上是考查同学们的识图能力.图中的点的横坐标表示时间,所以点E点距离家最远,横坐标表示距家最远的时间,纵坐标表示离家的距离;休息是路程不在随时间的增加而增加;往返全程中回来时候速度最快,用距离除以所用时间即可;用玲玲全程所行的路程除以所用的时间即可.
试题解析:观察图象可知:(1)玲玲到离家最远的地方需要3小时,此时离家30千米;
(2)10点半时开始第一次休息;休息了半小时;
(3)玲玲在返回的途中最快,速度为:30÷(15﹣13)=15千米/小时;
(4)玲玲全程骑车的平均速度为:(30+30)÷(15﹣9)=10千米/小时.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】⊙O的半径为6cm,点A到圆心O的距离为5cm,那么点A与⊙O的位置关系是( )
A. 点A在圆内 B. 点A在圆上 C. 点A在圆外 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
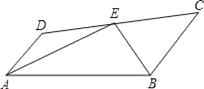
【题目】如图:E在线段CD上,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x﹣3)2+|y﹣4|=0.
(1)求AD和BC的长;
(2)你认为AD和BC还有什么关系?并验证你的结论;
(3)你能求出AB的长度吗?若能,请写出推理过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形、矩形、正方形都具有的性质是( )
A. 对角线相等且互相平分 B. 对角线相等且互相垂直平分
C. 对角线互相平分 D. 四条边相等,四个角相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com