
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
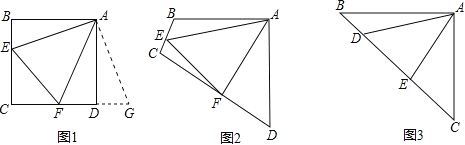
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___________,SAS
易证△AFG≌___________△AEF
,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°.点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系______________∠B+∠D=180°
时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
【答案】答案见解析.
【解析】
试题分析:(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,再证明△AFG≌△AFE进而得到EF=FG,即可得EF=BE+DF;
(2)∠B+∠D=180°时,EF=BE+DF,与(1)的证法类同;
(3)根据△AEC绕点A顺时针旋转90°得到△ABE′,根据旋转的性质,可知△AEC≌△ABE′得到BE′=EC,AE′=AE,∠C=∠ABE′,∠EAC=∠E′AB,根据Rt△ABC中的,AB=AC得到∠E′BD=90°,所以E′B2+BD2=E′D2,证△AE′D≌△AED,利用DE=DE′得到DE2=BD2+EC2;
试题解析:(1)∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中
 ,
,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF.
(2)∠B+∠D=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,

∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中
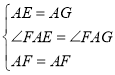 ,
,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF.
(3)猜想:DE2=BD2+EC2,
证明:连接DE′,根据△AEC绕点A顺时针旋转90°得到△ABE′,

∴△AEC≌△ABE′,
∴BE′=EC,AE′=AE,
∠C=∠ABE′,∠EAC=∠E′AB,
在Rt△ABC中,
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴∠ABC+∠ABE′=90°,
即∠E′BD=90°,
∴E′B2+BD2=E′D2,
又∵∠DAE=45°,
∴∠BAD+∠EAC=45°,
∴∠E′AB+∠BAD=45°,
即∠E′AD=45°,
在△AE′D和△AED中,
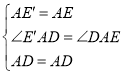
∴△AE′D≌△AED(SAS),
∴DE=DE′,
∴DE2=BD2+EC2.


科目:初中数学 来源: 题型:
【题目】探究证明:
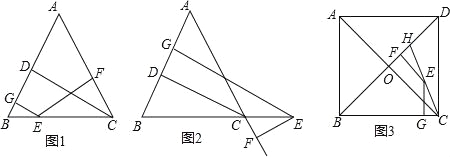
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图像经过点(-1.-5),且与正比例函数y=![]() x的图象相交于点(2,m).
x的图象相交于点(2,m).
(1)求m的值;
(2)求一次函数y=kx+b的解析式;
(3)求这两个函数图像与x轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2009年1 月的利润为200万元.设2009年1 月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2009年1 月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
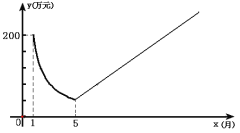
⑴分别求该化工厂治污期间及治污改造工程完工后y与x之间对应的函数关系式.
⑵治污改造工程完工后经过几个月,该厂月利润才能达到2009年1月的水平?
⑶当月利润少于100万元时为该厂资金紧张期,问该厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+![]() x=﹣
x=﹣![]() ,…第一步
,…第一步
x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,…第二步
)2,…第二步
(x+![]() )2=
)2=![]() ,…第三步
,…第三步
x+![]() =
=![]() (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x=![]() ,…第五步
,…第五步
嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)、如图(1),AB∥CD,点P在AB、CD外部,若∠B=40°,∠D=15°,则∠BPD °.
(2)、如图(2),AB∥CD,点P在AB、CD内部,则∠B,∠BPD,∠D之间有何数量关系?证明你的结论;
(3)、在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com