
分析 (1)令h=0,将二次函数转化为方程x2-(2m-1)x+m2-m=0求根的问题,根据方程根的判别式来证明;
(2)首先令h=x2-(2m-1)x+m2-m=0,求出x1=m,x2=m-1,然后结合题意得到y=2-$\frac{2(m-1)}{m}$=$\frac{2}{m}$,由y>m-1来求m的取值范围.
解答 解:∵b2-4ac=[-(2m-1)2]-4×(m2-m),
=1>0,
∴不论m取何值时,该二次函数图象总与x轴有两个交点;
(2)令h=0,则x2-(2m-1)x+m2-m=0,
整理,得
(x-m)[x-(m-1)]=0.
∵x1>x2,
∴x1=m,x2=m-1,
∴y=2-$\frac{2(m-1)}{m}$=$\frac{2}{m}$,
∴y>m-1,即$\frac{2}{m}$<m-1,
∴m<-1或0<m<2.
点评 本题考查的是抛物线与x轴的交点,根的判别式,解答此题的时,也可以利用数形结合的思想画出函数图象,再根据函数图象直接解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
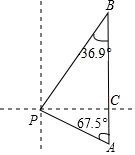 马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.
马航MH370 客机“失联”,我国“海巡01号”前往搜寻.如图某天上午9时,“海巡01号”轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西36.9°方向,求轮船行驶过程中与小岛P的最短距离PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
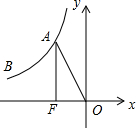 如图,已知反比例函数的图象经过点A(-2,4)、B(m,2),过点A作AF⊥x轴于点F,连接OA.
如图,已知反比例函数的图象经过点A(-2,4)、B(m,2),过点A作AF⊥x轴于点F,连接OA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
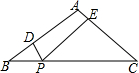 △ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )| A. | 4.8 | B. | 4.8或3.8 | C. | 3.8 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com