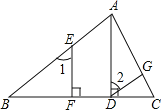
[题目]完成下列证明:如图.已知AD⊥BC.EF⊥BC.∠1=∠2．求证:DG∥BA．证明:∵AD⊥BC.EF⊥BC∴∠EFB=90°.∠ADB=90°( )∴∠EFB=∠ADB∴EF∥AD( )∴∠1=∠BAD( )又∵∠1=∠2∴∠ =∠ ∴DG∥BA．( )．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】完成下列证明：如图，已知AD⊥BC，EF⊥BC，∠1=∠2．

求证：DG∥BA．

证明：∵AD⊥BC，EF⊥BC（已知）

∴∠EFB=90°，∠ADB=90°（______）

∴∠EFB=∠ADB（等量代换）

∴EF∥AD（______）

∴∠1=∠BAD（______）

又∵∠1=∠2（已知）

∴∠______=∠______（等量代换）

∴DG∥BA．（______）．

【答案】垂直定义；同位角相等，两直线平行；两直线平行，同位角相等；∠2＝∠BAD；内错角相等，两直线平行

【解析】

试题先根据垂直的定义证得∠EFB=90°，∠ADB=90°，再根据平行线的判定和性质依次分析即可.

∵AD⊥BC，EF⊥BC ( 已知 )

∴∠EFB=90°，∠ADB=90°(__垂直定义___ )

∴∠EFB=∠ADB ( 等量代换 )

∴EF∥AD (同位角相等，两直线平行)

∴∠1=∠BAD (两直线平行，同位角相等)

又∵∠1=∠2 ( 已知)

∴∠2＝∠BAD（等量代换）

∴DG∥BA (内错角相等，两直线平行) .

练习册系列答案

中考专项突破系列答案

全能金卷小学毕业升学全程总复习系列答案

新课程同步导学练测八年级英语下册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】2020年春节，一场新冠病毒疫情由武汉开始席卷了整个中华地区，全国人民齐心协力、共同抗疫．为了防止感染，口罩成为了大众纷纷抢购的必需品，由于需求增加导致价格不断走高，引起了民众与政府的高度关注，据统计：2020年2月份一盒口罩价格比2020年1月份上涨了，某市民2020年2月3日在某超市订购了一盒口罩花了52元．

（1）问：2020年1月份一盒口罩的价格为多少元？

（2）某超市将进货价为每盒39元的口罩，按2020年2月3日价格出售，平均一天能销售出100盒，经调查表明：口罩的售价每盒下降1元，其口罩销售量就增加10盒，超市为了实现销售口罩每天有1320元的利润，并且尽可能让顾客得到实惠，每盒口罩的售价应该下降多少元？

查看答案和解析>>

科目：初中数学 来源： 题型：

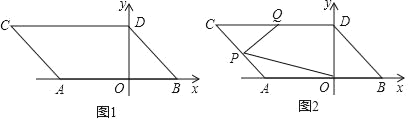
【题目】如图1，在平面直角坐标系中，点A，B的坐标分别为A(a，0)，B(b，0)，且a，b满足|2a+6|+(2a﹣3b+12)2＝0，现同时将点A，B分别向左平移2个单位，再向上平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD．

(1)请直接写出A，B两点的坐标；

(2)如图2，点P是线段AC上的一个动点，点Q是线段CD的中点，连接PQ，PO，当点P在线段AC上移动时(不与A，C重合)，请找出∠PQD，∠OPQ，∠POB的数量关系，并证明你的结论；

(3)在坐标轴上是否存在点M，使三角形MAD的面积与三角形ACD的面积相等？若存在，直接写出点M的坐标；若不存在，试说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

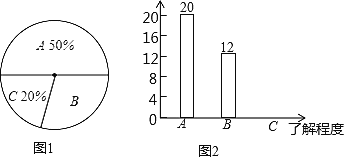
【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉；B:了解较多；C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:

(1)求小刚所在的班级共有多少名学生；

(2)在条形图中,将表示“一般了解”的部分补充完整‘’

(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数；

(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我们知道，任意一个正整数都可以进行这样的分解:(是正整数，且)，在的所有这种分解中，如果两因数之差的绝对值最小，我们就称是的最佳分解并规定:，例如:12可以分解成1×12、2×6、3×4，因为：

，所以3×4是12的最佳分解，所以F(12)=

(1)求F(18)-F(16)的值；

(2)若正整数是4的倍数，我们称正整数为“四季数”，如果一个两位正整数

(，为自然数)，交换个位上的数字与十位上的数字得到的新两位正整数减去原来的两位正整数所得的差为“四季数”，那么我们称这个数为“有缘数”，求所有“有缘数”中的最小值.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．

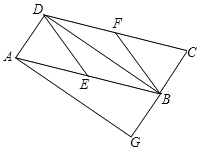
（1）求证：△ADE≌△CBF；

（2）若四边形 BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某中学在今年4月23日的“世界读书日”开展“人人喜爱阅读，争当阅读能手”活动，同学们积极响应，涌现出大批的阅读能手．为了激励同学们的阅读热情，养成每天阅读的好习惯，学校对阅读能手进行了奖励表彰，计划用2700元来购买甲、乙、丙三种书籍共100本作为奖品，已知甲、乙、丙三种书的价格比为2：2：3，甲种书每本20元．

（1）求出乙、丙两种书的每本各多少元？

（2）若学校购买甲种书的数量是乙种书的1.5倍，恰好用完计划资金，求甲、乙、丙三种书各买了多少本？

（3）在活动中，同学们表现优秀，学校决定提升奖励档次，增加了245元的购书款，在购买书籍总数不变的情况下，求丙种书最多可以买多少本？

（4）七（1）班阅读氛围浓厚，同伴之间交换书籍共享阅读，已知甲种书籍共270页，小明同学阅读甲种书籍每天21页，阅读5天后，发现同伴比他看得快，为了和同伴及时交换书籍，接下来小明每天多读了a页（20＜a＜40），结果再用了b天读完，求小明读完整本书共用了多少天？