
分析 先把1.4变为$\sqrt{1.96}$,再根据实数大小比较的方法比较即可求解;
先把$\sqrt{7}$变为$\root{6}{343}$,$\root{3}{20}$变为$\root{6}{400}$,再根据实数大小比较的方法比较即可求解.
解答 解:∵1.4=$\sqrt{1.96}$,2>1.96,
∴$\sqrt{2}$>1.4;
∵$\sqrt{7}$=$\root{6}{343}$,$\root{3}{20}$=$\root{6}{400}$,343<400,
∴$\sqrt{7}$<$\root{3}{20}$.
故答案为:>;<.
点评 此题主要考查了实数的大小比较,解答此题的关键对$\sqrt{2}$和1.4,$\sqrt{7}$和$\root{3}{20}$进行整理,再进行比较.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
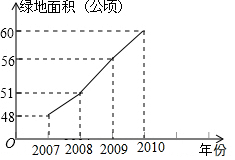 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房、植树、种草、修建公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.某市城区近几年来,通过拆迁旧房、植树、种草、修建公园等措施,使城区绿地面积不断增加(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{27}$÷$\sqrt{3}$=3 | C. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com