
 如图,在平面直角坐标系xOy中,直线$y=-\frac{{2\sqrt{3}}}{3}x+4$交y轴于点A,交x轴于点B,以线段AB为边作菱形ABCD(点C、D在第一象限),且点D的纵坐标为9.
如图,在平面直角坐标系xOy中,直线$y=-\frac{{2\sqrt{3}}}{3}x+4$交y轴于点A,交x轴于点B,以线段AB为边作菱形ABCD(点C、D在第一象限),且点D的纵坐标为9.分析 (1)分别令一次函数中x=0、y=0,求出与之对应的y、x的值,由此即可得出点A、B的坐标;
(2)过点D作DE⊥y轴,垂足为E,由点D的纵坐标为9即可得出AE的长,根据菱形的性质得出AB=AD,结合勾股定理即可求出点D的坐标,由DC∥AB可设直线DC的解析式为$y=-\frac{{2\sqrt{3}}}{3}x+b$,代入点D的坐标求出b值即可得出结论;
(3)假设存在,点C时以BD为对角线找出的点,再分别以AB、AD为对角线,根据平行四边形的性质(对角线互相平分)结合点A、B、D的坐标即可得出点P的坐标.
解答 解:(1)令$y=-\frac{{2\sqrt{3}}}{3}x+4$中x=0,则y=4,
∴点A(0,4);
令$y=-\frac{{2\sqrt{3}}}{3}x+4$中y=0,则-$\frac{2\sqrt{3}}{3}$x+4=0,解得:x=2$\sqrt{3}$,
∴点B($2\sqrt{3}$,0).
(2)过点D作DE⊥y轴,垂足为E,如图1所示.
∵点D的纵坐标为9,OA=4,
∴AE=5.
∵四边形是ABCD是菱形,
∴AD=AB=$\sqrt{O{A^2}+O{B^2}}=\sqrt{{4^2}+{{(2\sqrt{3})}^2}}=2\sqrt{7}$,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{28-25}$=$\sqrt{3}$,
∴D($\sqrt{3}$,9).
∵四边形是ABCD是菱形,
∴DC∥AB,
∴设直线DC的解析式为$y=-\frac{{2\sqrt{3}}}{3}x+b$,
∵直线DC过点D($\sqrt{3}$,9),
∴b=11,
∴直线DC的解析式为$y=-\frac{{2\sqrt{3}}}{3}x+11$.
(3)假设存在.
以点A、B、D、P组成的四边形是平行四边形还有两种情况(如图2):
①以AB为对角线时,
∵A(0,4),B($2\sqrt{3}$,0),D($\sqrt{3}$,9),
∴点P(0+2$\sqrt{3}$-$\sqrt{3}$,4+0-9),即($\sqrt{3}$,-5);
②以AD为对角线时,
∵A(0,4),B($2\sqrt{3}$,0),D($\sqrt{3}$,9),
∴点P(0+$\sqrt{3}$-2$\sqrt{3}$,4+9-0),即(-$\sqrt{3}$,13).
故除点C外,在平面直角坐标系xOy中还存在点P,使点A、B、D、P组成的四边形是平行四边形,点P的坐标为($\sqrt{3}$,-5)或(-$\sqrt{3}$,13).
点评 本题考查了一次函数图象上点的坐标特征、菱形的性质、勾股定理以及待定系数法求函数解析,解题的关键是:(1)分别代入x=0、y=0,求出与之对应的y、x的值;(2)求出点D的坐标;(3)分别以AB、AD为对角线求出点P的坐标.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形的性质(对角线互相平分),结合三个顶点的坐标求出另一顶点坐标是关键.


科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ABC=90°,将AB边绕点A逆时针旋转90°得到线段AD,将AC边绕点C顺时针旋转90°后得到线段CE,AE与BD交于点F,若DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则BC边的长为$\sqrt{7}$-1.
如图,在△ABC中,∠ABC=90°,将AB边绕点A逆时针旋转90°得到线段AD,将AC边绕点C顺时针旋转90°后得到线段CE,AE与BD交于点F,若DF=$\sqrt{2}$,EF=2$\sqrt{2}$,则BC边的长为$\sqrt{7}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平行四边形ABCD在平面直角坐标系中的位置如图所示,已知AB=8,AD=6,∠BAD=60°,点A的坐标为(-2,0).求:
平行四边形ABCD在平面直角坐标系中的位置如图所示,已知AB=8,AD=6,∠BAD=60°,点A的坐标为(-2,0).求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,长方形ABCD中,AB=5cm,AD=9cm,现将该长方形沿BC方向平移,得到长方形A1B1C1D1,若重叠部分A1B1CD的面积为20cm2,则长方形ABCD向右平移的距离为5cm.
如图,长方形ABCD中,AB=5cm,AD=9cm,现将该长方形沿BC方向平移,得到长方形A1B1C1D1,若重叠部分A1B1CD的面积为20cm2,则长方形ABCD向右平移的距离为5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
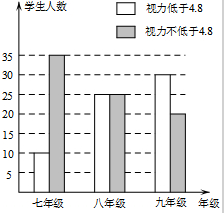 在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:
在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com