
����Ŀ��ij���������в�ר��ij��Ʒ����ÿ���ɱ�ÿ���ɱ�30Ԫ���ӿ�ҵһ��ʱ���ÿ������ͳ���У������ȡһ����������±���ʾ��
���۵�λ��Ԫ�� | 50 | 60 | 70 | 75 | 80 | 85 | �� |
�������� | 300 | 240 | 180 | 150 | 120 | 90 | �� |
����ÿ�춨�������Dz���ģ���ÿ������������������ֹ��ɣ�
��1�����������������ۼ۸�֮������ĺ�����ϵʽ��
��2�����в�ԭ�趨��������Ա�������������ϴ�ʱ����ÿ���۳�������198��ʱ�����������һ��ӪҵԱ���ܱ�֤Ӫҵ������У���ӪҵԱÿ��ÿ�칤��Ϊ40Ԫ����ÿ����ƷӦ���۶���Ԫ������ʹÿ�����в����������������=�����۩��ɱ���ӪҵԱ���ʣ�
���𰸡�
��1���⣺����ͼ�����ݷ������������������ۼ۸�֮��ĺ�����ϵΪһ�κ�����
��y=kx+b��������50��300������60��240����
���뺯����ϵʽ�ã� ![]() ��
��
��ã�k=��6��b=600��
��y=��6x+600��
��2���⣺��ÿ����ƷӦ����xԪ������ΪW��
����������y��198ʱ����6x+600��198��
��ã�x��67��
������ã�W=��x��30��������6x+600����2��40
=��6x2+780x��18080
=��6��x��65��2+7270
��x��67��
��xȡ67ʱ��Wȡ�����W���=7246Ԫ��
����������y��198ʱ����6x+600��198��
��ã�x��67��
������ã�W=��x��30��������6x+600����3��40
=��6x2+780x��18120
=��6��x��65��2+7230
��30��x��67��
��xȡ65ʱ��Wȡ�����W���=7230Ԫ��
���Ͽɵã���ÿ����ƷӦ����67Ԫ������ʹÿ�����в����������
����������1���۲�������ݣ���֪�������������ۼ۸�֮��ĺ�����ϵΪһ�κ������������������ʽ��
��2��������=ÿ��������![]() �۳�������-���ʡ�����δ֪�����ֶν���������ϵʽ������������꣬�ٸ��ݸ������⣬����Ա�����ȡֵ��Χ��������⡣
�۳�������-���ʡ�����δ֪�����ֶν���������ϵʽ������������꣬�ٸ��ݸ������⣬����Ա�����ȡֵ��Χ��������⡣
�����㾫����ͨ���������ȷ��һ�κ����ı���ʽ�Ͷ��κ�������ֵ������ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ����������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a�����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
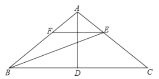
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��D��BC���ϵ��е㣬����AD��BEƽ�֡�ABC��AC�ڵ�E����E��EF��BC��AB�ڵ�F��
��1������C=36�㣬���BAD�Ķ�����
��2����֤��FB=FE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��F��AC����AE=CF��
֤����DE=BF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=9���Ѿ���ABCD�ضԽ���BD�۵���ʹ��C���F�غϣ�BF��AD�ڵ�M������C��CE��BF�ڵ�E����AD�ڵ�G����MG�ij�= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���������̼������ɫ���У��������ƻ�������ͼ��ʾ���������ţ����ŵĸ���10�ף�ԭ������б�ǡ�CAB=45�㣮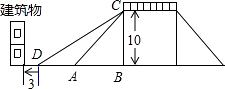
��1������������б�ǡ�CDB=28�㣬��������ij�CD���Ƕ��٣�����ȷ��0.1�ף�
��2�������½Ƕ���Dǰ��3�����е���Ҫʹ��ԭ�½Ƕ���A��10�Ľ����ﲻ��������������б�ǡ�CDB��������Сֵ�Ƕ��٣�����ȷ��1�㣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�У�ABΪ��O��ֱ����AB=4��PΪAB��һ�㣬����P����O����CD�����BCD=m��ACD��
��1����֪ ![]() ����m��ֵ������BCD����ACD�Ķ������Ƕ��٣�
����m��ֵ������BCD����ACD�Ķ������Ƕ��٣�
��2���ڣ�1���������£��� ![]() ������CD�ij���
������CD�ij���
��3���� ![]() ʱ���Ƿ������ʵ��m��ʹ��CD��̣�������ڣ����m��ֵ����������ڣ�˵�����ɣ�
ʱ���Ƿ������ʵ��m��ʹ��CD��̣�������ڣ����m��ֵ����������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У���ACBΪ��ǣ���DΪ����BC��һ���㣬����AD����ADΪһ������AD���Ҳ���������ADEF������������⣺
��1�����AB=AC����BAC=90��
�ٵ���D���߶�BC��ʱ�����B���غϣ�����ͼ2���߶�CF��BD֮���λ�ù�ϵΪ �� ������ϵΪ ��
�ڵ���D���߶�BC���ӳ�����ʱ����ͼ3�����еĽ����Ƿ���Ȼ������Ϊʲô��
��2����ͼ4�����AB��AC����BAC��90�㣬��D���߶�BC���˶�����AC=4 ![]() ��BC=3����BCA=45�㣬������ADEF�ı�DE���߶�CF�ཻ�ڵ�P�����߶�CP�������ֵ��
��BC=3����BCA=45�㣬������ADEF�ı�DE���߶�CF�ཻ�ڵ�P�����߶�CP�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OAC����BAD���ǵ���ֱ�������Σ���ACO=��ADB=90��������������y=![]() �ڵ�һ����ͼ����B������OAC����BAD�����֮��S��OAC��S��BADΪ��������
�ڵ�һ����ͼ����B������OAC����BAD�����֮��S��OAC��S��BADΪ��������

A. 36 B. 12 C. 6 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬��OAB=30�ȣ�
��1�����APB�Ķ�����
��2����OA=3ʱ����AP�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com