
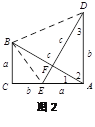
【题目】(本题7分)如图,在Rt△ABC中,∠ACB=90°,E为AC上一点,且AE=BC,过点A作AD⊥CA,垂足为A,且AD=AC,AB、DE交于点F.
(1)判断线段AB与DE的数量关系和位置关系,并说明理由;
(2)连接BD、BE,若设BC=a,AC=b,AB=c,请利用四边形ADBE的面积证明勾股定理.

【答案】(1)AB=DE,AB⊥DE.理由见解析;(2)证明见解析.
【解析】试题分析:(1)根据垂直的定义可证得∠DAE=∠ACB=90°,然后根据ASA可证△ABC≌△DEA,从而得证AB=DE,且∠3=∠1,然后根据直角三角形的内角和等量代换可证得AB⊥DE;
(2)根据三角形的面积和四边形的面积,可知S四边形ADBE= S△ADE+ S△BDE,S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2可得证符合勾股定理的逆定理.
b2可得证符合勾股定理的逆定理.
试题解析:(1)解:AB=DE, AB⊥DE.
如图2,∵AD⊥CA,∴∠DAE=∠ACB=90°,
∵AE=BC,∠DAE=∠ACB,AD=AC,∴△ABC≌△DEA,∴AB=DE,
∠3=∠1,∵∠DAE=90°,∴∠1+∠2=90°,∴∠3+∠2=90°,
∴∠AFE=90°,∴AB⊥DE.
(2)如图2,∵S四边形ADBE= S△ADE+ S△BDE=![]() DE·AF+
DE·AF+![]() DE·BF=
DE·BF=![]() DE·AB =
DE·AB =![]() c2,
c2,
S四边形ADBE=S△ABE+S△ADB=![]() a2+
a2+![]() b2,
b2,
∴![]() a2+
a2+![]() b2=
b2=![]() c2,∴a2+b2=c2.
c2,∴a2+b2=c2.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.同旁内角互补
B.一组数据的方差越大,这组数据波动性越大
C.若∠α=72°55′,则∠α的补角为107°45'
D.对角线互相垂直的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,|4-(-2)|表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离;同理|x-3|也可理解为x与3两数在数轴上所对应的两点之间的距离,试探索并完成填空.
(1)求|4-(-2)|=______,|-3-5|=______;
(2)若|x-2|=5,则x=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com