
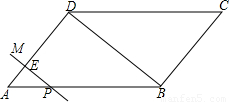
 .(2分)
.(2分) ;(4分)
;(4分)
 ,QF=
,QF= t,
t, ,PG=
,PG= +
+ t.
t. t+
t+ ;(8分)
;(8分)
 ,
, ,QF=
,QF= t,BP=t-6,CP=10-t,PG=(10-t)
t,BP=t-6,CP=10-t,PG=(10-t) ,
, ,故此时两平行线截平行四边形ABCD的面积为S=-
,故此时两平行线截平行四边形ABCD的面积为S=- t2+10
t2+10 t-34
t-34 ,(10分)
,(10分)
 ,
, .
. .(14分)
.(14分) ;
; ,(1分)
,(1分) ,(舍去),(2分)
,(舍去),(2分) ,(3分)
,(3分) .(4分)
.(4分)

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源:2005年四川省绵阳市中考数学试卷(大纲卷)(解析版) 题型:选择题
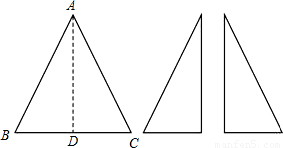
查看答案和解析>>
科目:初中数学 来源:2005年四川省绵阳市中考数学试卷(大纲卷)(解析版) 题型:选择题
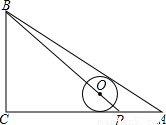

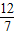

查看答案和解析>>
科目:初中数学 来源:2005年四川省绵阳市中考数学试卷(大纲卷)(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2004年四川省资阳市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com