
分析 ①首先对二次根式化简,然后进行乘法计算;
②首先利用分配律计算,然后化简二次根式,合并同类二次根式即可;
③利用加减法即可求解;
④利用加减法即可求解;
⑤把两组数代入方程,解方程组即可求解;
⑥首先计算0次幂,化简二次根式,然后合并同类二次根式即可.
解答 解:①原式=$\sqrt{3}$(2$\sqrt{3}$-4$\sqrt{3}$)=$\sqrt{3}$×(-2$\sqrt{3}$)=-6;
②原式=3$\sqrt{2}$-6$\sqrt{5}$-3$\sqrt{2}$=-6$\sqrt{5}$;
③$\left\{\begin{array}{l}{x+y=5…(1)}\\{2x-y=1…(2)}\end{array}\right.$,
(1)+(2)得3x=6,
解得:x=2,
把x=2代入(1)得2+y=5,
解得y=3,
则方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$;
④$\left\{\begin{array}{l}{x+3y=-1…(1)}\\{3x-2y=8…(2)}\end{array}\right.$,
3×(1)-(2)得11y=-11,
解得y=-1,
把y=-1代入(1)得x-3=-1,
解得x=2,
则方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
⑤根据题意得:$\left\{\begin{array}{l}{a-3=b}\\{2=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=5}\\{b=2}\end{array}\right.$;
⑥原式=-1-2$\sqrt{3}$+3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=-1+$\frac{2\sqrt{3}}{3}$.
点评 本题考查了二次根式的混合运算,正确对二次根式进行化简是关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:解答题
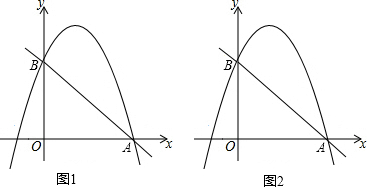
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于 CD长为半径画弧,两弧交于点P,作射线OP,由作法得△OCP≌△ODP的根据是( )
尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于 CD长为半径画弧,两弧交于点P,作射线OP,由作法得△OCP≌△ODP的根据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.03mm | B. | 0.02mm | C. | 30.03mm | D. | 29.92mm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com