练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，∠AOC为直角，OC是∠BOD的平分线，且∠AOB＝35°，求∠AOD的度数．

    145° 【解析】试题分析：首先根据∠AOB的度数和∠AOC的度数求出∠BOC的度数，根据角平分线的性质得出∠COD的度数，最后根据∠AOD=∠AOC+∠COD求出答案． 试题解析：【解析】 ∵∠AOC为直角，∴∠AOC＝90°， ∴∠BOC＝∠AOC－∠AOB＝90°－35°＝55°， 又OC平分∠BOD，∴∠COD＝∠BOC＝55°，∴∠AOD＝∠AOC＋∠COD＝9...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年北师大版七年级数学上册：第5章 一元一次方程 单元测试卷 题型：填空题

    一个两位数，个位数字是十位数字的4倍，如果把个位数字与十位数字对调，那么得到的新数比原数大54，则原数为________．

    28 【解析】【解析】 设原数十位数字为x，则个位数字为4x，根据题意可得： 40x+x﹣（10x+4x）=54，解得：x=2，故4x=8． 故原数为28．故答案为：28．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县九年级（上）期末数学试卷（五四学制） 题型：解答题

    某百货商店服装柜在销售中发现：某品牌童装每天可售出20件，每件盈利40元，经市场调查发现，在进货价不变的情况下，若每件童装每降价1元，日销售量将增加2件．

    （1）当每件童装降价多少元时，一天的盈利最多？

    （2）若商场要求一天的盈利为1200元，同时又使顾客得到实惠，每件童装降价多少元？

    （1）最大值为1250元；（2）每件童装降价20元． 【解析】试题分析：（1）设每件童装降价x元，则每天盈利为S，根据盈利=（每件盈利）×（销售件数）即可解题； （2）当S=1200时，即可求得x的值，即可解题． 试题解析：（1）设每件童装降价x元，则每天盈利为S， 则S=（40﹣x）（2x+20）=﹣2x2+60x+800， 当x==15时，S有最大值为1250元；...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省大庆市杜尔伯特县九年级（上）期末数学试卷（五四学制） 题型：单选题

    把抛物线y=﹣2x2向上平移1个单位，再向右平移1个单位，得到的抛物线是（　　）

    A. y=﹣2（x+1）2+1 B. y=﹣2（x﹣1）2+1 C. y=﹣2（x﹣1）2﹣1 D. y=﹣2（x+1）2﹣1

    B 【解析】试题解析：∵函数y=-2x2的顶点为（0，0）， ∴向上平移1个单位，再向右平移1个单位的顶点为（1，1）， ∴将函数y=-2x2的图象向上平移1个单位，再向右平移1个单位，得到抛物线的解析式为y=-2（x-1）2+1， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：解答题

    如图①，将一副三角板的两个锐角顶点放到一块，∠AOB＝45°，∠COD＝30°，OM，ON分别是∠AOC，∠BOD的平分线．

    (1)当∠COD绕着点O逆时针旋转至射线OB与OC重合时(如图②)，则∠MON的大小为________；

    (2)如图③，在(1)的条件下，继续绕着点O逆时针旋转∠COD，当∠BOC＝10°时，求∠MON的大小，写出解答过程；

    (3)在∠COD绕点O逆时针旋转过程中，∠MON＝________°.

    （1）37.5°；（2）∠MON=37.5°；（3）37.5° 【解析】试题分析：(1)、根据角平分线的性质得出∠NOC=15°，∠MOC=22.5°，最后根据∠MON=∠NOC+∠MOC得出答案；(2)、首先根据∠BOC的度数求出∠AOC和∠BOD的度数，然后根据角平分线的性质求出∠BON和∠MOB的度数，最后根据∠MON=∠MOB+∠BON得出答案；(3)、根据题意得出∠AOC＝∠AOB...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：填空题

    如图，图中的线段共有________条，直线共有________条．

    3 1 【解析】试题分析：根据线段和直线的性质可知：本图中的线段有：线段BC，线段CD和线段BD，共3条；直线有：直线BD，共1条．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学北师大版上册：第4章 基本平面图形 单元测试卷 题型：单选题

    如图，一条流水生产线上L1、L2、L3、L4、L5处各有一名工人在工作，现要在流水生产线上设置一个零件供应站P，使五人到供应站P的距离总和最小，这个供应站设置的位置是(　　)

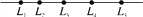
    A. L2处 B. L3处 C. L4处 D. 生产线上任何地方都一样

    B 【解析】试题分析：设在L3处为最佳，求出此时的总距离为L1L5+L2L4，假如设于任意的X处，求出总距离为L1L5+L2L4+L3X，和L1L5+L2L4比较即可． 【解析】 在5名工人的情况下，设在L3处为最佳，这时总距离为L1L5+L2L4， 理由是：如果不设于L3处，而设于X处，则总距离应为L1L5+L2L4+L3X＞L1L5+L2L4， 即在L3处5个工人到供...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型：填空题

    一个凸多边形的内角和与外角和相等，它是______边形．

    四． 【解析】设这个正多边形的边数是n，则（n-2）•180°=360°，解得n=4．所以这个正多边形是四边形．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版八年级数学下册练习：第十八章达标检测卷 题型：解答题

    如图，△ABC中，AB＝AC＝1，∠BAC＝45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE，CF相交于点D。

    （1）求证：BE＝CF ；

    （2）当四边形ACDE为菱形时，求BD的长。

    （1）证明见解析（2）-1 【解析】试题分析：（1）先由旋转的性质得AE=AB，AF=AC，∠EAF=∠BAC，则∠EAF+∠BAF=∠BAC+∠BAF，即∠EAB=∠FAC，利用AB=AC可得AE=AF，于是根据旋转的定义，△AEB可由△AFC绕点A按顺时针方向旋转得到，然后根据旋转的性质得到BE=CD； （2）由菱形的性质得到DE=AE=AC=AB=1，AC∥DE，根据等腰三角形的...

    查看答案和解析>>

    同步练习册答案