
【题目】某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,点C关于原点O的对称点为点D,连接CD,BC,BD,求△BCD的面积.
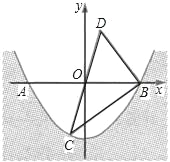
【答案】(1) ![]() (2) 15
(2) 15
【解析】【试题分析】(1)以抛物线的对称轴为y轴,AB=8,则B(4,0),将点B代入即可.
(2)先代入二次函数表达式,求出点C的坐标C(﹣1,﹣![]() ),再求出关于原点的对称点D的坐标(1,
),再求出关于原点的对称点D的坐标(1,![]() ),最后再求出两个三角形的面积和.
),最后再求出两个三角形的面积和.
【试题解析】
(1)∵AB=8,由抛物线的性质可知OB=4,
∴B(4,0),
把B点坐标代入解析式得:16a﹣4=0,
解得:a=![]() ;
;
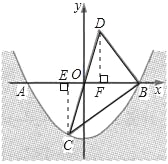
(2)过点C作CE⊥AB于E,过点D作DF⊥AB于F,
∵a=![]() ,
,
∴y=![]() x2﹣4,
x2﹣4,
令x=﹣1,
∴m=![]() ×(﹣1)2﹣4=﹣
×(﹣1)2﹣4=﹣![]() ,
,
∴C(﹣1,﹣![]() ),
),
∵C关于原点对称点为D,
∴D的坐标为(1,![]() ),
),
则CE=DF=![]() ,
,
S△BCD=S△BOD+S△BOC=![]() OBDF+
OBDF+![]() OBCE=
OBCE=![]() ×4×
×4×![]() +
+![]() ×4×
×4×![]() =15,
=15,
∴△BCD的面积为15平方米.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边上的中点,连结AC、BD,回答问题
(1)对角线AC、BD满足条件_____时,四边形EFGH是矩形.
(2)对角线AC、BD满足条件_____时,四边形EFGH是菱形.
(3)对角线AC、BD满足条件_____时,四边形EFGH是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:BM=CM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当矩形ABCD的长和宽满足什么条件时,四边形MENF是正方形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次排列的3个数:3,9,8,对任相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,![]() ,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,
,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,![]() ,
,![]() ,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
,9,8,继续依次操作下去,问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,AF与DE相交于点G,BF与CE相交于点H.
(1)求证:四边形EHFG是平行四边形;
(2)①若四边形EHFG是菱形,则平行四边形ABCD必须满足条件 ;
②若四边形EHFG是矩形,则平行四边形ABCD必须满足条件 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边BC在x轴上,且∠ACB=90°.反比例函数y=![]() (x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
(x>0)的图象经过AB边的中点D,且与AC边相交于点E,连接CD.已知BC=2OB,△BCD的面积为6.
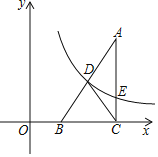
(1)求k的值;(2)若AE=BC,求点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
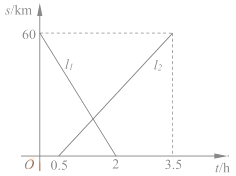
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com