
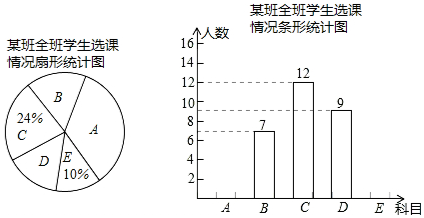
分析 (1)用C组的人数除以它所占的百分比即可得到全班人数,先计算出E组人数和A组人数,然后补全频数分布直方图;
(2)用E组的所占百分比乘以360°即可得到在扇形统计图中“E”对应扇形的圆心角的度数;
(3)先画树状图展示所有12种等可能的结果数,找出选出的2人恰好1人选修篮球,1人选修足球所占结果数,然后根据概率公式求解.
解答 解:(1)该班的总人数为12÷24%=50(人),
E科目人数为50×10%=5(人),A科目人数为50-(7+12+9+5)=17(人),
补全图形如下: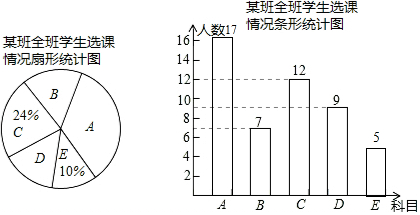
故答案为:50;
(2)表示“足球”所在扇形的圆心角是360°×$\frac{7}{50}$=50.4°,
故答案为:50.4;
(3)画树状图为: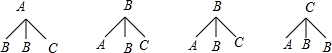
共有12种等可能的结果数,其中选出的2人恰好1人选修篮球,1人选修足球占4种,
所以选出的2人恰好1人选修篮球,1人选修足球的概率=$\frac{4}{12}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查条形统计图与扇形统计图.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
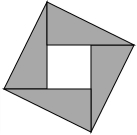 2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则(a+b)2的值为( )| A. | 25 | B. | 19 | C. | 13 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 7 | D. | 无数个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
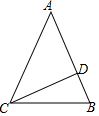 从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.
从等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的黄金分割线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com