
【题目】如图,已![]() 是
是![]() 的边
的边![]() 上的一点,
上的一点,![]() ,
,![]() =
=![]() ,
,![]() 是
是![]() 的中线.
的中线.
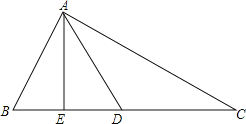
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求证:![]() 是
是![]() 的平分线.
的平分线.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据已知条件得到∠BAD=∠BDA=60°,于是得到AB=AD,等量代换得到CD=AD,根据等腰三角形的性质得到∠DAC=∠C,推出∠BDA=∠DAC+∠C=2∠C,即可得到结论;
(2)证明:延长AE到M,使EM=AE,连接DM,推出△ABE≌△MDE,根据全等三角形的性质得到∠B=∠MDE,AB=DM,根据全等三角形的判定定理得到△MAD≌△CAD,根据全等三角形的性质得到∠MAD=∠CAD,即可得到结论.
(1)解:∵∠B=60°,∠BDA=∠BAD,
∴∠BAD=∠BDA=60°,
∴AB=AD,
∵CD=AB,
∴CD=AD,
∴∠DAC=∠C,
∴∠BDA=∠DAC+∠C=2∠C,
∵∠BAD=60°,
∴∠C=30°;
(2)证明:延长AE到M,使EM=AE,连接DM,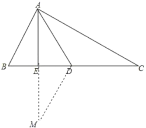
在△ABE和△MDE中,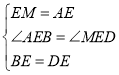 ,
,
∴△ABE≌△MDE,
∴∠B=∠MDE,AB=DM,
∵∠ADC=∠B+∠BAD=∠MDE+∠BDA=∠ADM,
在△MAD与△CAD,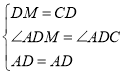 ,
,
∴△MAD≌△CAD,
∴∠MAD=∠CAD,
∴AD是∠EAC的平分线.


科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整
如图,已知AD⊥BC于D,点E在BA的延长线上,EG⊥BC于C,交AC于点F,∠E=∠1.求证:AD平分∠BAC.

证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=∠EGC=90°( ),
∴AD∥EG( ),
∴∠1=∠2( ),
∴_____=∠3( ),
又∵∠E=∠1(已知),∴∠2=∠3( ),
∴AD平分∠BAC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD,DE.

(1)求证:D是BC的中点;
(2)若DE=3,BD-AD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠DAB=90°,且∠ABC=60°,AB=AC,△ADC的外接圆⊙O交BC于点E,连接DE并延长交AB延长线于点F.

(1)求证:CF=DB;
(2)当AD=![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68°方向上,航行2小时后到达N处,观测灯塔P在西偏南46°方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68°≈0.9272,sin46°≈0.7193,sin22°≈0.3746,sin44°≈0.6947)( )

A. 22.48海里 B. 41.68海里 C. 43.16海里 D. 55.63海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)
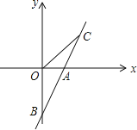
(1)求直线AB所对应的函数关系式;
(2)若直线AB上一点C在第一象限且点C的坐标为(a,2),求△BOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com