
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 . 
【答案】2或5
【解析】解:∵Rt△ABC纸片中,∠C=90°,AC=6,BC=8,
∴AB=10,
∵以AD为折痕△ABD折叠得到△AB′D,
∴BD=DB′,AB′=AB=10.
如图1所示:当∠B′DE=90°时,过点B′作B′F⊥AF,垂足为F.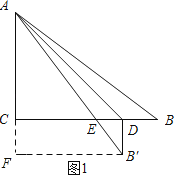
设BD=DB′=x,则AF=6+x,FB′=8﹣x.
在Rt△AFB′中,由勾股定理得:AB′2=AF2+FB′2 , 即(6+x)2+(8﹣x)2=102 .
解得:x1=2,x2=0(舍去).
∴BD=2.
如图2所示:当∠B′ED=90°时,C与点E重合.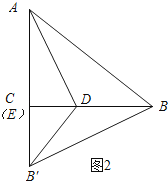
∵AB′=10,AC=6,
∴B′E=4.
设BD=DB′=x,则CD=8﹣x.
在Rt△′BDE中,DB′2=DE2+B′E2 , 即x2=(8﹣x)2+42 .
解得:x=5.
∴BD=5.
综上所述,BD的长为2或5.
所以答案是:2或5.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.
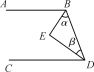
完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
A.点C
B.点D或点E
C.线段DE(异于端点) 上一点
D.线段CD(异于端点) 上一点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.

(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为![]() 秒.
秒.
①若△NPH的面积为1,求![]() 的值;
的值;
②点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com