Question

3．已知O是△ABC的外心，∠BAC=45°，延长BC至D，使CD=$\frac{1}{2}$BC，AD∥OC，求∠ABC的度数．

Answer 1

分析 分两种情况：①当△ABC是锐角三角形时；由圆周角定理得出∠BOC=90°，设BO延长交AD于E，由已知条件得出∠AEO=90°，OE=$\frac{1}{2}$OA，得出∠OAE=30°，因此∠AOE=60°，由圆周角定理得出∠ABE=$\frac{1}{2}$∠AOE=30°，再由等腰直角三角形的性质得出∠OBC=45°，即可得出∠ABC的度数；
②当△ABC是钝角三角形时；同①得：∠ABE=30°，∠OBC=45°，∠ABC=∠OBC-∠ABE，即可得出结果．

解答 解：分两种情况：
①当△ABC是锐角三角形时；
连接OA、OB、OC，如图1所示：
∵∠BAC=45°，
∴∠BOC=90°，
设BO延长交AD于E，
∵AD∥OC，CD=$\frac{1}{2}$BC，
∴OE=$\frac{1}{2}$OB，∠AEO=90°，
∴OE=$\frac{1}{2}$OA，
∴∠OAE=30°，
∴∠AOE=60°，
∴∠ABE=$\frac{1}{2}$∠AOE=30°，
∵OA=OB=OC，
∴∠OBC=∠OCB=45°，
∴∠ABC=∠OBC+∠OBA=75°；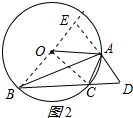
②当△ABC是钝角三角形时；
连接OA、OB、OC，如图2所示：
∵∠BAC=45°，
∴∠BOC=90°，
设BO延长交AD于E，
同①得：∠ABE=30°，∠OBC=45°，
∴∠ABC=∠OBC-∠ABE=45°-30°=15°；
综上所述：∠ABC的度数为75°或15°．

点评 本题考查了圆周角定理、等腰直角三角形的性质、含30°角的直角三角形的判定、平行线的性质；本题综合性强，有一定难度，需要进行分类讨论．