
【题目】如图,AB 是⊙O 的直径,点C 是⊙O 上一点,AD 与过点C的切线垂直,垂足为 D,直线 DC 与AB 的延长线相交于点P,弦CE 平分∠ACB,交AB 于点F,连接BE.

求证:(1)AC 平分∠DAB;
(2)△PCF 是等腰三角形.
【答案】详见解析.
【解析】试题分析:
(1)由已知条件证AD∥OC可得∠DAC=∠ACO;由OA=OC可得∠ACO=∠CAO;两者结合可得∠DAC=∠CAO,从而可得AC平分∠DAB;
(2)由AD⊥DC,AB 是⊙O 的直径,可得∠ADC=∠ACB=90°,从而可得∠DAC+∠DCA=∠DCA+∠PCB=90°,这样可得∠DAC=∠PCB=∠CAO;由CE平分∠ACB可得∠ACF=∠BCF,这样可得∠CAO+∠ACF=∠PCB+∠BCF,结合三角形外角性质可证得:∠PCF=∠PFC,从而可得PC=PF,就可得△PCF是等腰三角形.
试题解析:
(1)∵ PD 切⊙O 于点C,
∴OC⊥PD,
又AD⊥PD,
∴OC∥AD,
∴∠ACO=∠DAC,
又OC=OA,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC 平分∠DAB.
(2)∵AD⊥PD,
∴∠DAC+∠ACD=90°,
又AB 为⊙O 的直径,
∴∠ACB=90°,
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB,
又∠DAC=∠CAO,
∴∠CAO=∠PCB,
∵CE 平分∠ACB,
∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF,
∴△PCF 是等腰三角形.


科目:初中数学 来源: 题型:
【题目】设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,
(1)试推导x1+x2=-![]() ,x1·x2=
,x1·x2=![]() ;
;
(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
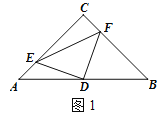
【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 抛掷一枚硬币,硬币落地时正面朝上是随机事件
B. 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件
C. 任意打开七年级下册数学教科书,正好是97页是确定事件
D. 一个盒子中有白球m个,红球6个,黑球n个(每个除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在⊙O中,AB= 4![]() ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.

⑴求图中阴影部分的面积;
⑵若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥底面圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某企业决定购买10台污水处理设备;现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
处理污水量(吨/月) | 240 | 200 |
年消耗费(万元/台) | 1 | 1 |
经预算,该企业购买设备的资金不高于105万元。
(1) 请你设计该企业有几种购买方案;
(2)若该企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD的四个顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).
(1)试计算四边形ABCD的面积;
(2)若将该四边形各顶点的横坐标都加2,纵坐标都加3,其面积怎么变化?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com