
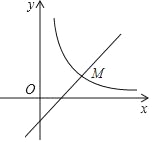
【题目】如图,一次函数y=x﹣2与反比例函数y=![]() (x>0)的图象相交于点M(m,1).
(x>0)的图象相交于点M(m,1).
(1)填空:m的值为 ,反比例函数的解析式为 ;
(2)已知点N(n,n),过点N作l1∥x轴,交直线y=x﹣2于点A,过点N作l2∥y轴,交反比例函数y=![]() (x>0)的图象与点B,试用n表示△NAB的面积S.
(x>0)的图象与点B,试用n表示△NAB的面积S.
【答案】(1)3,y=![]() ;(2)|
;(2)|![]() ﹣n|.
﹣n|.
【解析】分析:(1)把M(m,1)代入一次函数y=x-2,可得m的值;把M(3,1)代入反比例函数y=![]() (x>0),可得k的值;
(x>0),可得k的值;
(2)依据点N与点A的纵坐标相同,均为n,可得AN=n+2-n=2,依据点N与点B的横坐标相同,均为n,可得BN=|![]() -n|,即可得到S△NBA=
-n|,即可得到S△NBA=![]() ×2×|
×2×|![]() -n|=|
-n|=|![]() -n|.
-n|.
详解:(1)把M(m,1)代入一次函数y=x-2,可得
1=m-2,
解得m=3,
把M(3,1)代入反比例函数y=![]() (x>0),可得
(x>0),可得
k=3×1=3,
∴反比例函数的解析式为y=![]() ,
,
(2)由题可得,点N与点A的纵坐标相同,均为n,
将y=n代入y=x-2中,得x=n+2,
∴A(n+2,n),
∴AN=n+2-n=2,
由题可得,点N与点B的横坐标相同,均为n,
将x=n代入y=![]() 中,得y=
中,得y=![]() ,
,
∴B(n,![]() ),
),
∴BN=|![]() -n|,
-n|,
∴S△NBA=![]() ×2×|
×2×|![]() -n|=|
-n|=|![]() -n|.
-n|.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
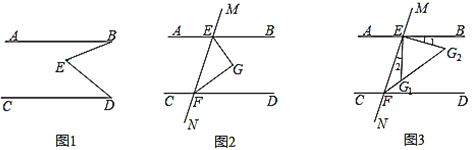
【题目】已知,直线AB∥CD.
(1)如图1,若点E是AB、CD之间的一点,连接BE.DE得到∠BED.求证:∠BED=∠B+∠D.
(2)若直线MN分别与AB、CD交于点E.F.
①如图2,∠BEF和∠EFD的平分线交于点G.猜想∠G的度数,并证明你的猜想;
②如图3,EG1和EG2为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点G1和G2.求证:∠FG1E+∠G2=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD平分∠ACB交AB于点D,E为AC上一点,且DE=CE.
(1)求证:DE∥BC;
(2)若∠A=90°,S△BCD=26,BC=13,求AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国七十周年华诞,某校举行书画大赛,准备购买甲、乙两种文具,奖励在活动中表现优秀的师生.已知购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元;购买
元;购买![]() 个甲种文具、
个甲种文具、![]() 个乙种文具共需花费
个乙种文具共需花费![]() 元.
元.
(1)求购买一个甲种文具、一个乙种文具各需多少元?
(2)若学校计划购买这两种文具共![]() 个,投入资金不少于
个,投入资金不少于![]() 元又不多于
元又不多于![]() 元,设购买甲种文具
元,设购买甲种文具![]() 个,求有多少种购买方案?
个,求有多少种购买方案?
(3)设学校投入资金![]() 元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
元,在(2)的条件下,哪种购买方案需要的资金最少?最少资金是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD,顶点D恰好落在双曲线y=![]() .若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )
.若将正方形沿x轴向左平移b个单位长度后,点C恰好落在该双曲线上,则b的值为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:数学兴趣一小组的同学对完全平方公式进行研究:因![]() ,将左边展开得到
,将左边展开得到![]() ,移项可得:
,移项可得:![]() .
.
数学兴趣二小组受兴趣一小组的启示,继续研究发现:对于任意两个非负数![]() 、
、![]() ,都存在
,都存在![]() ,并进一步发现,两个非负数
,并进一步发现,两个非负数![]() 、
、![]() 的和一定存在着一个最小值.
的和一定存在着一个最小值.
根据材料,解答下列问题:
(1)![]() __________(
__________(![]() ,
,![]() );
);![]() ___________(
___________(![]() );
);
(2)求![]() 的最小值;
的最小值;
(3)已知![]() ,当
,当![]() 为何值时,代数式
为何值时,代数式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2)点M是边BC上的一个动点(不与B、C重合),反比例函数![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
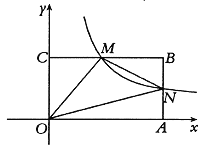
(1)当点M是边BC的中点时,求反比例函数的表达式;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一批衬衫,每件进价![]() 元,开始以每件
元,开始以每件![]() 元的价格销售,每星期能卖出
元的价格销售,每星期能卖出![]() 件,后来因库存积压,决定降价销售,经两次降价后的每件售价
件,后来因库存积压,决定降价销售,经两次降价后的每件售价![]() 元,每星期能卖出
元,每星期能卖出![]() 件.
件.
![]() 已知两次降价百分率相同,求每次降价的百分率;
已知两次降价百分率相同,求每次降价的百分率;
![]() 聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低
聪明的店主在降价过程中发现,适当的降价既可增加销售又可增加收入,且每件衬衫售价每降低![]() 元,销售会增加
元,销售会增加![]() 件,若店主想要每星期获利
件,若店主想要每星期获利![]() 元,应把售价定为多少元?
元,应把售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角三角形ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求![]() 的值.
的值.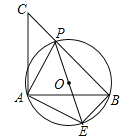
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com