
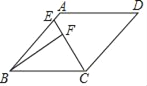
【题目】如图,在菱形ABCD中,∠ABC=45°,AB=4,点E是AB边上的动点,过点B作直线CE的垂线,垂足为点F.
(1)当点F落在AB上时,求∠BCF的度数;
(2)若∠EBF=15°,求CF的长;
(3)当点E从点A运动到点B时,求点F运动的路径长.
【答案】(1)∠BCF=45°(2)2或2![]() (3)
(3)![]()
【解析】分析:(1)根据等腰直角三角形的性质即可解决问题;
(2)分以下两种情况:①当点F在菱形内部时,②当点F在菱形外部时;
(3)首先确定点F的运动轨迹,利用弧长公式计算即可;
详解:(1)当点F落在AB上时,点E,F重合,即CF⊥AB.
∵∠ABC=45°,∴∠BCF=45°.
(2)分以下两种情况:
①当点F在菱形内部时,∠FBC=45°﹣15°=30°.在Rt△BFC中,BC=4,∠FBC=30°,sin30°=![]() =
=![]() ,∴CF=2;
,∴CF=2;
②当点F在菱形外部时,∠FBC=15°+45°=60°.在Rt△BFC中,BC=4,sin60°=![]() =
=![]() ,∴CF=2
,∴CF=2![]() .
.
故CF的长为2或2![]() .
.
(3)如图,设BC的中点为点O,以点O为圆心,OB长为半径画半圆O,连
接 AC,BD交于点F′,易得点F′在半圆O上,连接OF′.
∵BF⊥CE,∴∠BFC=90°,∴点F在半圆O中的一段弧上运动,当点E从点A运动到点B时,点F的运动路径的长为![]() 的长.
的长.
∵∠ABC=45°,∴∠BCF′=67.5°,∴∠BOF′=135°,∴![]() 的长为
的长为![]() =
=![]() .
.



 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】某同学模仿二维码的方式为学校设计了一个身份识别图案系统:在![]() 的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为
的正方形网格中,黑色正方形表示数字1,白色正方形表示数字0.如图1是某个学生的身份识别图案.约定如下:把第i行,第j列表示的数字记为![]() (其中i,j=1,2,3,4),如图1中第2行第1列的数字
(其中i,j=1,2,3,4),如图1中第2行第1列的数字![]() =0;对第i行使用公式
=0;对第i行使用公式![]() 进行计算,所得结果
进行计算,所得结果![]() 表示所在年级,
表示所在年级,![]() 表示所在班级,
表示所在班级,![]() 表示学号的十位数字,
表示学号的十位数字,![]() 表示学号的个位数字.如图1中,第二行
表示学号的个位数字.如图1中,第二行![]() ,说明这个学生在5班.
,说明这个学生在5班.
(1)图1代表的学生所在年级是______年级,他的学号是_________;
(2)请仿照图1,在图2中画出八年级4班学号是36的同学的身份识别图案

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图1),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,现将三角板EFG绕O点顺时针旋转,旋转角![]() 满足条件
满足条件![]() 四边形CHGK是旋转过程中两三角板的重叠部分(如图2).
四边形CHGK是旋转过程中两三角板的重叠部分(如图2).
(1)在上述旋转过程中,BH与CK有怎样的数量关系?证明你的结论;
(2)在上述旋转过程中,两个直角三角形的重叠部分面积是否会发生改变?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
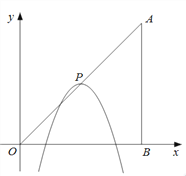
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(6,6)、(6,0).抛物线![]() 的顶点P在折线OAAB上运动.
的顶点P在折线OAAB上运动.
(1)当点P在线段OA上运动时,抛物线![]() 与y轴交点坐标为(0,c).
与y轴交点坐标为(0,c).
①用含m的代数式表示n;
②求c的取值范围;
(2)当抛物线![]() 经过点B时,求抛物线所对应的函数表达式.
经过点B时,求抛物线所对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
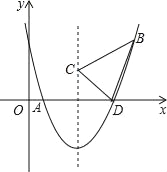
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读句画图并完成计算:如图,直线AB与直线CD交于点C ,

(1)过点P作PQ∥CD,交AB于点Q;
(2)过P作PR⊥CD于点R;
(3)若∠DCB=150,求∠PQC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
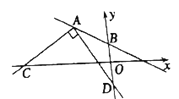
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣4,4),点B的坐标为(0,2).
(1)求直线AB的解析式;
(2)如图,以点A为直角顶点作∠CAD=90°,射线AC交x轴于点C,射线AD交y轴于点D.当∠CAD绕着点A旋转,且点C在x轴的负半轴上,点D在y轴的负半轴上时,OC﹣OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC, AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com