
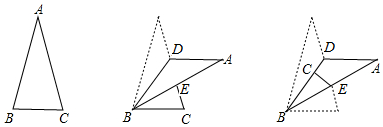
分析 在图①的△ABC中,根据三角形内角和定理,可求得∠B+∠C=150°;结合折叠的性质和图②③可知:∠B=3∠CBD,即可在△CBD中,得到另一个关于∠B、∠C度数的等量关系式,联立两式即可求得∠B的度数.
解答 解:在△ABC中,∠A=30°,则∠B+∠C=150°…①;
根据折叠的性质知:∠B=3∠CBE,∠BCE=∠C;
在△CBE中,则有:∠CBE+∠BCE=180°-78°,即:
| 1 |
| 3 |
| 2 |
| 3 |
点评 此题主要考查的是图形的折叠变换及三角形内角和定理的应用,能够根据折叠的性质发现∠B和∠CBD的倍数关系是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | -$\frac{1}{3}$ | C. | 0.080080008 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
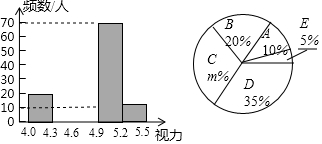 某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.| 组别 | 视力 | 频数(人) |
| A | 4.0≤x<4.3 | 20 |
| B | 4.3≤x<4.6 | a |
| C | 4.6≤x<4.9 | b |
| D | 4.9≤x<5.2 | 70 |
| E | 5.2≤x<5.5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
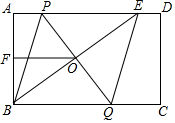 如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 组号 | ① | ② | ③ | ④ | ⑤ |
| 频数 | 8 | ■ | 15 | 10 | 11 |
| A. | 0.12 | B. | 0.6 | C. | 6 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com