
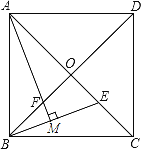
【题目】如图,正方形ABCD的边长为2![]() ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
(1)求证:AF=BE;
(2)求点E到BC边的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用ASA证明△AFO≌△BE,然后根据全等三角形的对应边相等即可得AF=BE;
(2)如图,过点E作EN⊥BC,垂足为N,根据正方形的边长求得对角线的长,继而求得OC的长且∠ECN=45°,由E是OC的中点,可得OE=EC=1,在直角三角形ENC中利用勾股定理进行求解即可得.
(1)∵正方形ABCD, ∴AO=BO,∠AOF=∠BOE=90°
∵AM⊥BE,∠AFO=∠BFM,∴∠FAO=∠EBO
在△AFO和△BEO中
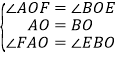 ,
,
∴△AFO≌△BE(ASA),
∴AF=BE;
(2)如图,过点E作EN⊥BC,垂足为N,

∵正方形ABCD的边长为2![]() ,
,
∴AC=![]() =4,CO=2,且∠ECN=45°,
=4,CO=2,且∠ECN=45°,
∵E是OC的中点,∴OE=EC=1,
由EN⊥BC,∠ECN=45°,得∠CEN=45°,
∴EN=CN,
设EN=CN=x,∵![]() +
+![]() =
=![]() ,
,
∴![]() +
+![]() =1 ,
=1 ,
∴![]() 因为x>0,x
因为x>0,x![]() ,
,
即:点E到BC边的距离是![]() .
.


科目:初中数学 来源: 题型:
【题目】探究规律,完成相关题目.
老师说:“我定义了一种新的运算,叫(加乘)运算.”
然后老师写出了一些按照(加乘)运算的运算法则进行运算的算式:
(+5)(+2)=+7;(-3)(-5)=+8;
(-3)(+4)=-7; (+5)(-6)=-11;
0(+8)=8;(-6)0=6.
小明看了这些算式后说:“我知道老师定义的(加乘)运算的运算法则了.”
聪明的你也明白了吗?
(1)归纳(加乘)运算的运算法则:
两数进行(加乘)运算时,运算法则是什么.
特别地,0和任何数进行(加乘)运算,或任何数和0进行(加乘)运算运算法则是什么.
(2)计算:
①(![]() )[
)[![]() (
(![]() )].(括号的作用与它在有理数运算中的作用一致)
)].(括号的作用与它在有理数运算中的作用一致)
② 若(![]() )(
)(![]()
![]() )
)![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为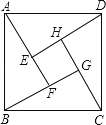
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第( )秒
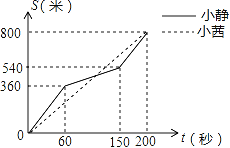
A. 80 B. 105 C. 120 D. 150
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4
B.2,3,2
C.3,2,0.4
D.3,3,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b和反比例函数y= ![]() 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 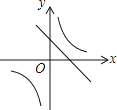
A.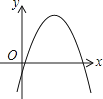
B.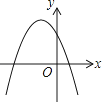
C.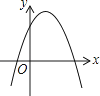
D.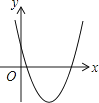
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的村料,再分解因式.
要把多项式![]() 分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得
分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得
![]() .
.
这时,由于![]() 中又有公困式
中又有公困式![]() ,于是可提公因式
,于是可提公因式![]() ,从而得到
,从而得到![]() ,因此有
,因此有
![]()
![]()
![]()
![]() .
.
这种因式分解的方法叫做分组分解法,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来因式分解.
请用上面材料中提供的方法因式分解:
![]()
![]() 请你完成分解因式下面的过程
请你完成分解因式下面的过程![]()
![]() ______
______
![]() ;
;
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com