
【题目】某中学组织学生去福利院献爱心,在准备礼品时发现,购买1个甲礼品比购买1个乙礼品多花40元,并且花费600元购买甲礼品和花费360元购买乙礼品的数量相等.
(1)向甲、乙两种礼品的单价各为多少元?
(2)学校准备购买甲、乙两种礼品共30个送给福利院的老人,要求购买礼品的总费用不超过2400元,那么最多可购买多少个甲礼品?
【答案】(1)甲礼品的单价为100元,乙礼品的单价为60元;(2)最多可购买15个甲礼品.
【解析】
(1)设购买一个乙礼品需要x元,根据“花费600元购买甲礼品和花费360元购买乙礼品的数量相等”列分式方程求解即可;
(2)设总费用不超过2400元,可购买m个甲礼品,则购买乙礼品(30-m)个,根据题意列不等式求解即可.
(1)设购买一个乙礼品需要x元,
根据题意得![]() =
=![]() ,
,
解得x=60,
经检验x= 60是原方程的根,
所以x+40= 100,
答:甲礼品的单价为100元,乙礼品的单价为60元;
(2)设总费用不超过2400元时,可购买m个甲礼品,(30- m)个乙礼品,
根据题意得100m+ 60(30- m)≤2400,
解得m≤15,
答:最多可购买15个甲礼品.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
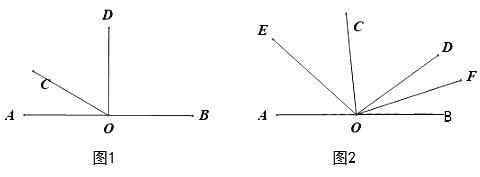
【题目】如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数;
(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;
(3)在(1)中线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当OD与OB重合时旋转都停止),OM、ON分别平分∠BOC、∠BOD,多少秒时∠COM=∠BON(直接写出答案,不必写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是射线BM上的一个动点(点P不与点B重合),∠AOB= 30°,∠ABM=60°.当∠OAP=______时,以点A、O、B中的任意两点和点P为顶点的三角形是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,DE垂直平分AB ,分别交AB、BC于点D 、E,MN垂直平分AC,分别交AC、BC于点M、N,连接AE,AN.
(1)如图1,若∠BAC= 100°,求∠EAN的度数;
(2)如图2,若∠BAC=70°,求∠EAN的度数;
(3)若∠BAC=a(a≠90°),请直接写出∠EAN的度数. (用含a的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
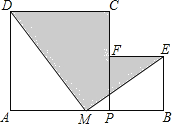
【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
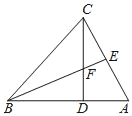
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE与BD交于点A.求证:
(1)BF=AC;
(2)BE是AC的中垂线;
(3)若AD=2,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com