
分析 ①方程利用直接开平方法求出解即可;
②方程利用配方法求出解即可;
③方程利用因式分解法求出解即可;
④方程利用因式分解法求出解即可;
⑤方程利用因式分解法求出解即可;
⑥方程利用配方法求出解即可.
解答 解:①(2x-1)2=9,
开方得:2x-1=3或2x-1=-3,
解得:x1=2,x2=-1;
②x2+3x-4=0,
方程变形得:x2+3x=4,
配方得:x2+3x+$\frac{9}{4}$=$\frac{25}{4}$,即(x+$\frac{3}{2}$)2=$\frac{25}{4}$,
开方得:x+$\frac{3}{2}$=±$\frac{5}{2}$,
解得:x1=1,x2=-4;
③x2-2x-8=0,
分解因式得:(x-4)(x+2)=0,
解得:x1=4,x2=-2;
④方程整理得:(x+4)2-5(x+4)=0,
分解因式得:(x+4)(x+4-5)=0,
解得:x1=-4,x2=1;
⑤方程整理得:(x+1)(x+2)-2(x+2)=0,
分解因式得:(x+2)(x+1-2)=0,
解得:x1=-2,x2=1;
⑥方程移项得:x2+2x=9999,
配方得:x2+2x+1=10000,即(x+1)2=10000,
开方得:x+1=100或x+1=-100,
解得:x1=99,x2=-101.
点评 此题考查了解一元二次方程-因式分解法,配方法,以及直接开平方法,熟练掌握各种解法是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
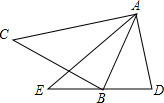 如图,在△ABC和△ADE中,∠CAB=∠EAD,AC=AE,
如图,在△ABC和△ADE中,∠CAB=∠EAD,AC=AE,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com