
如图1,点O是边长为1的等边△ABC内的任一点,设∠AOB= °,∠BOC=
°,∠BOC= °
°
(1)将△BOC绕点C沿顺时针方向旋转60°得△ADC,连结OD,如图2所示. 求证:OD=OC。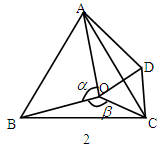
(2)在(1)的基础上,将△ABC绕点C沿顺时针方向旋转60°得△EAC,连结DE,如图3所示. 求证:OA=DE
(3)在(2)的基础上, 当 、
、 满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
(1)根据旋转的性质可得CO=CD,∠DOC=60°,即得△COD是等边三角形,问题得证;(2)根据旋转的性质可得△ADC≌△BOC,△EAC≌△ABC,则可得AD=BO,∠DAC=∠OBC,EA=AB,∠EAC=∠ABC,即可证得△EAD≌△ABO,问题得证;(3)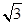
解析试题分析:(1)根据旋转的性质可得CO=CD,∠DOC=60°,即得△COD是等边三角形,问题得证;
(2)根据旋转的性质可得△ADC≌△BOC,△EAC≌△ABC,则可得AD=BO,∠DAC=∠OBC,EA=AB,∠EAC=∠ABC,即可证得△EAD≌△ABO,问题得证;
(3)根据全等三角形的性质可得∠ADC=∠BOC= ,∠EDA=∠AOB=
,∠EDA=∠AOB= ,即得∠CDE=
,即得∠CDE=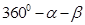 ,由△COD是等边三角形可得∠COD=∠CDO=60°,若点B、O、D、E在同一直线上,则∠BOC=∠CDE=120°,即
,由△COD是等边三角形可得∠COD=∠CDO=60°,若点B、O、D、E在同一直线上,则∠BOC=∠CDE=120°,即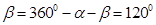 ,得
,得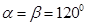 ,从而可以求得结果.
,从而可以求得结果.
(1)∵△BOC绕点C沿顺时针方向旋转60°得△ADC
∴CO=CD,∠DOC=60°
∴△COD是等边三角形
∴OD=OC;
(2)∵△BOC绕点C沿顺时针方向旋转60°得△ADC
△ABC绕点C沿顺时针方向旋转60°得△EAC
∴△ADC≌△BOC,△EAC≌△ABC
∴AD=BO,∠DAC=∠OBC,EA=AB,∠EAC=∠ABC
∴∠EAC-∠DAC=∠ABC-∠OBC即∠DAE=∠OBA
∴△EAD≌△ABO
∴OA=DE;
(3)∵△ADC≌△BOC,△EAD≌△ABO
∴∠ADC=∠BOC= ,∠EDA=∠AOB=
,∠EDA=∠AOB=
∴∠CDE=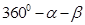
∵△COD是等边三角形
∴∠COD=∠CDO=60°
若点B、O、D、E在同一直线上,则∠BOC=∠CDE=120°
即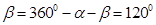 ,得
,得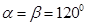
AO+BO+CO的最小值为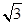 .
.
考点:旋转问题的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
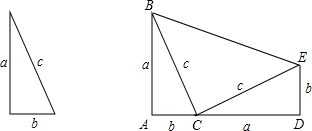 (1)如图,它可以看作是边长为a,b,c的两直角三角形成,其中A,B,C三点在同直线上,请从面积出发,写出一个a,b,c的等式;(要过程)
(1)如图,它可以看作是边长为a,b,c的两直角三角形成,其中A,B,C三点在同直线上,请从面积出发,写出一个a,b,c的等式;(要过程)查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江杭州余杭九年级下学期阶段性测试数学试卷(解析版) 题型:解答题
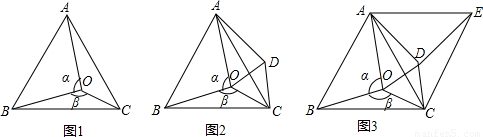
如图1,点O是边长为1的等边△ABC内的任一点,设∠AOB= °,∠BOC=
°,∠BOC= °
°

(1)将△BOC绕点C沿顺时针方向旋转60°得△ADC,连结OD,如图2所示. 求证:OD=OC。

(2)在(1)的基础上,将△ABC绕点C沿顺时针方向旋转60°得△EAC,连结DE,如图3所示. 求证:OA=DE

(3)在(2)的基础上, 当 、
、 满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
满足什么关系时,点B、O、D、E在同一直线上。并直接写出AO+BO+CO的最小值。
查看答案和解析>>
科目:初中数学 来源:2013年浙江省杭州市中考数学预测试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com