
【题目】已知反比例函数y=![]() 的图象与一次函数y=k2x+m的图象交于A(a,1)、B(
的图象与一次函数y=k2x+m的图象交于A(a,1)、B(![]() ,﹣3)两点,连结AO.
,﹣3)两点,连结AO.
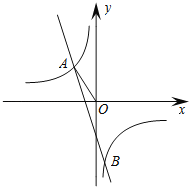
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出k2x+m﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标.
【答案】(1)反比例函数关系式为y=﹣![]() ,一次函数关系式为y=﹣3x﹣2;(2)﹣1<x<0或x>
,一次函数关系式为y=﹣3x﹣2;(2)﹣1<x<0或x>![]() ;(3)点C的坐标为:(0,﹣
;(3)点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() )或(0,2)或(0,1).
)或(0,2)或(0,1).
【解析】
试题分析:(1)将点A(﹣1,a)、B(![]() ,﹣3)代入反比例函数y=
,﹣3)代入反比例函数y=![]() 中得:﹣3×
中得:﹣3×![]() =(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(
=(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(![]() ,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
(2)根据图象得到一次函数在反比例函数下方时x的取值范围即可求解;
(3)分三种情况:①OA=OC;②AO=AC;③CA=CO;讨论可得点C的坐标.
解:(1)∵反比例函数y=![]() 的图象经过B(
的图象经过B(![]() ,﹣3),
,﹣3),
∴k1=3×![]() ×(﹣3)=﹣3,
×(﹣3)=﹣3,
∵反比例函数y=![]() 的图象经过点A(﹣1,a),
的图象经过点A(﹣1,a),
∴a=1.
由直线y2=k2x+m过点A,B得: ,
,
解得![]() .
.
∴反比例函数关系式为y=﹣![]() ,一次函数关系式为y=﹣3x﹣2;
,一次函数关系式为y=﹣3x﹣2;
(2)k2x+m﹣![]() <0的x的取值范围为﹣1<x<0或x>
<0的x的取值范围为﹣1<x<0或x>![]() ;
;
(3)OA=![]() =
=![]() ,
,
如图,线段OA的垂直平分线与y轴的交点,有1个,点C的坐标为:(0,1);
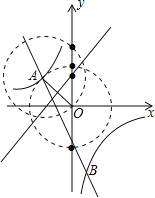
以点A为圆心、AO长为半径的圆与y轴的交点,有1个,点C的坐标为:(0,2);
以点O为圆心、OA长为半径的圆与y轴的交点,有2个,点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() ).
).
故点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() )或(0,2)或(0,1).
)或(0,2)或(0,1).


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:初中数学 来源: 题型:
【题目】有些大数值问题可以通过用字母代替数转化成整式问题来解决,请先阅读下面的解题过程,再解答下面的问题.
例:若x=123456789×123456786,y=123456788×123456787,试比较x、y的大小.
解:设123456788=a,那么x=(a+1)(a-2)=a2-a-2,y=a(a-1)=a2-a,
∵x-y=(a2-a-2)-(a2-a)=-2,∴x<y
看完后,你学到了这种方法吗?再亲自试一试吧,你准行!
问题:若x=20072007×20072011-20072008×20072010,
y=20072008×20072012-20072009×20072011,若设20072007=a,试用类似方法比较x、y的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
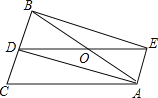
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球绕太阳公转的速度约是110 000千米/时,将110 000用科学记数法表示为( )
A. 11×104 B. 1.1×105 C. 1.1×104 D. 0.11×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农场老板准备建造一个矩形羊圈ABCD,他打算让矩形羊圈的一面完全靠着墙MN,墙MN可利用的长度为25m,另外三面用长度为50m的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
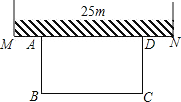
(1)若要使矩形羊圈的面积为300m2,则垂直于墙的一边长AB为多少米?
(2)农场老板又想将羊圈ABCD的面积重新建造成面积为320m2,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com