
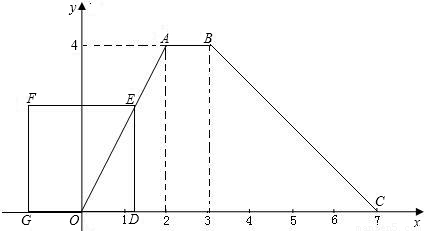
 时,此时OD=t,DE=7-t,重合部分的面积可由正方形的面积减去未重合的直角三角形的面积,由此求得S、t的函数关系式;
时,此时OD=t,DE=7-t,重合部分的面积可由正方形的面积减去未重合的直角三角形的面积,由此求得S、t的函数关系式; 时,此时重合部分的面积就是正方形EFGD的面积,从而求得S、t的函数关系式;
时,此时重合部分的面积就是正方形EFGD的面积,从而求得S、t的函数关系式; ,
, ;
; ;
; (7分)
(7分) 时,有:
时,有: ;
; 时,s的值小于
时,s的值小于 .(8分)
.(8分) 时,有:s=(t-7)2;
时,有:s=(t-7)2; ,(9分)
,(9分) .(10分)
.(10分)

 同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源: 题型:
| 8 |
| 3 |
| 16 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:2011年广东省茂名市化州市文楼镇第一中学中考数学二模试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com