ЃЈ1ЃЉНЋЕуAЃЈ2ЃЌ4ЃЉДњШыy=-x+bЃЌ
ЕУ4=-2+bЃЌНтЕУb=6ЃЌ
Ёрy=-x+6ЃЌ
ЕБy=0ЪБЃЌx=6ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ6ЃЌ0ЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈ6ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉЂйЩшжБЯпy=-x+6гыyжсНЛгкЕуDЃЌдђDЃЈ0ЃЌ6ЃЉЃЌ
ЁпBЃЈ6ЃЌ0ЃЉЃЌ
ЁрOB=OD=6ЃЌЁЯOBD=ЁЯODB=45ЁуЃЎ
Й§ЕуAЃЈ2ЃЌ4ЃЉзїANЁЭOBгкNЃЌдђAN=OC=4ЃЌON=AC=2ЃЌBN=AN=4ЃЌ
ЁрЕБЕуPЕНДяЕуCЪБЃЌЕуMЕНДяЕуNЃЎ
ЗжСНжжЧщПіЬжТлЃК
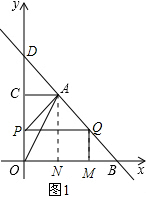
ЃЈiЃЉЕБ0ЁмtЁм4ЪБЃЌЕуPдкOCЩЯЃЌЕуQдкBAЩЯЃЌШчЭМ1ЃЎ
ЁпOP=tЃЌBM=QM=tЃЌ
ЁрPQ
ЁЮOBЃЌPQ=OM=OB-BM=6-tЃЌCP=OC-OP=4-tЃЌ
ЁрS=
PQ•CP=
ЃЈ6-tЃЉЃЈ4-tЃЉ=
t
2-5t+12ЃЛ
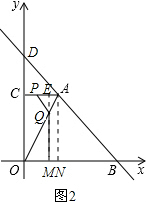
ЃЈiiЃЉЕБ4ЃМtЁм6ЪБЃЌЕуPдкACЩЯЃЌЕуQдкAOЩЯЃЌШчЭМ2ЃЌбгГЄMQНЛACгкЕуEЃЎ
ЁпOC+CP=tЃЌBM=tЃЌ
ЁрAP=6-tЃЌOM=OB-BM=6-tЃЎ
ЁпtanЁЯAON=
=
ЃЌ
Ёр
=
ЃЌ
ЁрQM=12-2tЃЌ
ЁрQE=EM-QM=4-ЃЈ12-2tЃЉ=2t-8ЃЌ
ЁрS=
AP•QE=
ЃЈ6-tЃЉЃЈ2t-8ЃЉ=-t
2+10t-24ЃЎ
злЩЯПЩжЊЃЌS=
| | t2-5t+12(0ЁмtЁм4) | | -t2+10t-24(4ЃМtЁм6) |
| |
ЃЛ
ЂкДцдквдMЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыSЯрЕШЃЌРэгЩШчЯТЃК
ЗжСНжжЧщПіЬжТлЃК
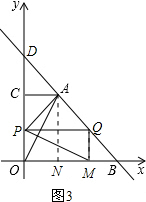
ЃЈiЃЉЕБ0ЁмtЁм4ЪБЃЌЕуPдкOCЩЯЃЌЕуQдкBAЩЯЃЌШчЭМ3ЃЎ
ЁпS
ЁїMPQ=
PQ•QM=
ЃЈ6-tЃЉt=-
t
2+3tЃЌS=
t
2-5t+12ЃЌ
Ёр-
t
2+3t=
t
2-5t+12ЃЌ
ећРэЃЌЕУt
2-8t+12=0ЃЌ
НтЕУt
1=2ЃЌt
2=6ЃЈВЛКЯЬтвтЩсШЅЃЉЃЛ
ЃЈiiЃЉЕБ4ЃМtЁм6ЪБЃЌЕуPдкACЩЯЃЌЕуQдкAOЩЯЃЌШчЭМ4ЃЎ
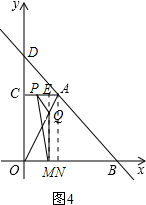
ЁпQM=12-2tЃЌPE=|CE-CP|=|ЃЈ6-tЃЉ-ЃЈt-4ЃЉ|=|10-2t|ЃЌ
ЁрS
ЁїMPQ=
QM•PE=
ЃЈ12-2tЃЉ|10-2t|=ЃЈ6-tЃЉ|10-2t|ЃЌ
гжЁпS=
AP•QE=
ЃЈ6-tЃЉЃЈ2t-8ЃЉ=ЃЈ6-tЃЉЃЈt-4ЃЉЃЌ
ЁрЃЈ6-tЃЉ|10-2t|=ЃЈ6-tЃЉЃЈt-4ЃЉЃЌ
Ёпt=6ЪБЃЌMгыQжиКЯЃЌВЛКЯЬтвтЩсШЅЃЌ
Ёр10-2t=ЁРЃЈt-4ЃЉЃЌ
ЕБ10-2t=t-4ЪБЃЌt=
ЃЛ
ЕБ10-2t=-ЃЈt-4ЃЉЪБЃЌt=6ЩсШЅЃЎ
злЩЯПЩжЊЃЌДцдквдMЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыSЯрЕШЃЌДЫЪБtЕФжЕЮЊ2Лђ
ЃЎ


 ЁпBЃЈ6ЃЌ0ЃЉЃЌ
ЁпBЃЈ6ЃЌ0ЃЉЃЌ ЃЈiiЃЉЕБ4ЃМtЁм6ЪБЃЌЕуPдкACЩЯЃЌЕуQдкAOЩЯЃЌШчЭМ2ЃЌбгГЄMQНЛACгкЕуEЃЎ
ЃЈiiЃЉЕБ4ЃМtЁм6ЪБЃЌЕуPдкACЩЯЃЌЕуQдкAOЩЯЃЌШчЭМ2ЃЌбгГЄMQНЛACгкЕуEЃЎ ЂкДцдквдMЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыSЯрЕШЃЌРэгЩШчЯТЃК
ЂкДцдквдMЁЂPЁЂQЮЊЖЅЕуЕФШ§НЧаЮЕФУцЛ§гыSЯрЕШЃЌРэгЩШчЯТЃК ЁпQM=12-2tЃЌPE=|CE-CP|=|ЃЈ6-tЃЉ-ЃЈt-4ЃЉ|=|10-2t|ЃЌ
ЁпQM=12-2tЃЌPE=|CE-CP|=|ЃЈ6-tЃЉ-ЃЈt-4ЃЉ|=|10-2t|ЃЌ







