Question

如图，直线y=kx﹣2与x轴交于点A（1，0），与y轴交于点B，若直线AB上的点C在第一象限，且S_△BOC=3，求点C的坐标．

Answer 1

（﹣3，﹣8）

解析试题分析：先把A点坐标代入y=kx﹣2求出k=2，得到直线解析式为y=2x﹣2，再确定B点坐标为（0，﹣2），设C点坐标为（x，y）（x＜0，y＜0），然后根据三角形面积公式得到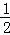×2×（﹣x）=3，解得x=﹣3，再求出自变量为﹣3所对应的函数值即可得到C点坐标．
试题解析：把A（1，0）代入y=kx﹣2得k﹣2=0，解得k=2，
∴直线解析式为y=2x﹣2，
把x=0代入y=2x﹣2得y=﹣2，
∴B点坐标为（0，﹣2），
设C点坐标为（x，y）（x＜0，y＜0），
∵S_△BOC=3，
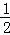∴×2×（﹣x）=3，解得x=﹣3，
把x=﹣3代入y=2x﹣2得y=﹣8，
∴C点坐标为（﹣3，﹣8）．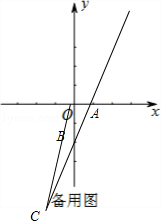

考点：一次函数图象上点的坐标特征．