Question

1．已知直角梯形ABCD中，∠ABC=90°，AB∥CD，AB=11，CD=6，BC=$\frac{5}{2}$，在Rt△EFG中，∠GEF=90°，EF=3，tanG=$\frac{1}{2}$，将△EFG与直角梯形ABCD如图（1）摆放，使点E与点A重合，EF与AB重合，△EFG与梯形ABCD在直线AB的同侧，现将△EFG沿射线AB向右以每秒1个单位的速度平移，当点C落在线段FG上时停止运动．在平移过程中，设△EFG与梯形ABCD的重叠部分的面积为S，运动时间为t秒（t≥0）．
（1）当点D落在线段FG上时，求出此时t值；
（2）请直接写出S与t的函数关系式，并注明对应自变量t的取值范围；
（3）当点C落在线段FG上时，将此时的△EFG沿FG翻折，得到△HFG，将△HFG绕点F旋转，在旋转过程中，设直线HG与直线AD交于点M，与直线AB交于点N，是否存在钝角△AMN为等腰三角形？若存在，求出此时AN的长；若不存在，请说明理由．

Answer 1

分析 （1）作垂线构建平行线，想办法求出AE的长，就是t的值；先根据三角函数值求GE的长，再利用平行线分线段成比例得比例式求FH的长，从而可以求EH的长，所以AE=AH-EH，得出结论；
（2）分四种情况讨论：①开始的位置，t=0，如图2，过M作MN⊥AB于N，过D作DH⊥AB于H，重叠部分的面积S就是△AFM的面积；②当0＜t≤$\frac{13}{4}$时，如图3，作辅助线，构建高线，重叠部分的面积S=S_△AFM-S_△AEP，计算即可；③当$\frac{13}{4}$＜t＜5时，如图4，重叠部分的面积S就是五边形PDFME的面积；④当5≤t＜8时，如图5，重叠部分的面积S就是梯形MEFN的面积；⑤当8≤t＜$\frac{37}{4}$时，如图6，重叠部分的面积S就是五边形PMQBE的面积；⑥当点C落在线段FG上时，如图7，t=$\frac{37}{4}$，重叠部分的面积S就是矩形MEBC的面积；
（3）分三种情况进行讨论，分别以A、M、N为顶角构成等腰三角形，要满足钝角三角形的有两种，分别求出AN的长即可．

解答 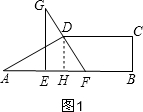解：（1）如图1，过D作DH⊥AB于H，则四边形DHBC为矩形，
∴AH=AB-CD=11-6=5，
在Rt△EFG中，∵EF=3，tanG=$\frac{1}{2}$，
∴$\frac{EF}{GE}=\frac{1}{2}$，即$\frac{3}{GE}=\frac{1}{2}$，
∴GE=6，
∵DH∥GE，
∴$\frac{DH}{GE}=\frac{FH}{EF}$，
∴$\frac{\frac{5}{2}}{6}=\frac{FH}{3}$，
∴FH=$\frac{5}{4}$，
∴EH=EF=FH=3-$\frac{5}{4}$=$\frac{7}{4}$，
∴AE=AH-EH=5-$\frac{7}{4}$=$\frac{13}{4}$，
∴当点D落在线段FG上时t=$\frac{13}{4}$；
（2）①当t=0时，如图2，过M作MN⊥AB于N，过D作DH⊥AB于H，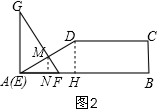
由tan∠G=$\frac{1}{2}$得tan∠NMF=$\frac{1}{2}$，设FN=x，则MN=2x，
∵MN∥DH，
∴$\frac{MN}{DH}$=$\frac{EN}{EH}$，
∴$\frac{2x}{\frac{5}{2}}$=$\frac{3-x}{5}$，
∴x=$\frac{3}{5}$，
∴MN=2x=$\frac{6}{5}$，
∴S=S_△EFM=$\frac{1}{2}$EF•MN=$\frac{1}{2}$×3×$\frac{6}{5}$=$\frac{9}{5}$；
②当0＜t≤$\frac{13}{4}$时，如图3，过M作MN⊥AB于N，过D作DH⊥AB于H，
设FN=x，则MN=2x，AN=3+t-x，
∵MN∥DH，
∴$\frac{MN}{DH}$=$\frac{AN}{AH}$，
∴$\frac{2x}{\frac{5}{2}}=\frac{3+t-x}{5}$，
∴x=$\frac{3+t}{5}$，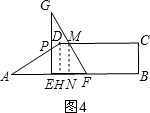
∴MN=$\frac{2（3+t）}{5}$，
由题意得：$\frac{DH}{AH}$=$\frac{PE}{AE}$，
∴$\frac{\frac{5}{2}}{5}$=$\frac{PE}{t}$，
∴PE=$\frac{1}{2}$t，
∴S=S_△AFM-S_△AEP，
=$\frac{1}{2}$AF•MN-$\frac{1}{2}$AE•EP，
=$\frac{1}{2}$（3+t）•$\frac{2（3+t）}{5}$-$\frac{1}{2}$t•$\frac{1}{2}$t，
=-$\frac{1}{20}$t²+$\frac{6}{5}$t+$\frac{9}{5}$；
③当$\frac{13}{4}$＜t＜5时，如图4，过M作MN⊥AB于N，过D作DH⊥AB于H，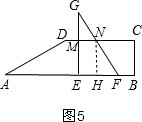
∵AE=t，AH=5，
∴FE=$\frac{t}{2}$，eh=5-t，
∵EN=$\frac{7}{4}$，FN=$\frac{5}{4}$，
∴NH=$\frac{7}{4}$-（5-t）=t-$\frac{13}{4}$，
∴S=S_梯形PEHD+S_矩形DHNM+S_△MNF，
=$\frac{1}{2}$×EH×（PE+DH）+DH×NH+$\frac{1}{2}$×MN×FN，
=$\frac{1}{2}$×（5-t）（$\frac{t}{2}$+$\frac{5}{2}$）+$\frac{5}{2}$（t-$\frac{13}{4}$）+$\frac{1}{2}$×$\frac{5}{2}$×$\frac{5}{4}$，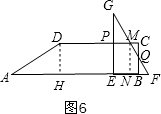
∴S$\left\{\begin{array}{l}{\frac{9}{5}（t=0）}\\{-\frac{1}{20}{t}^{2}+\frac{6}{5}t+\frac{9}{5}（0＜t≤\frac{13}{4}）}\\{-\frac{1}{4}{t}^{2}+\frac{5t}{2}-\frac{5}{16}（\frac{13}{4}＜t＜5）}\\{\frac{95}{16}（5≤t＜8）}\\{{t}^{2}-16t+\frac{1119}{16}（8≤t＜\frac{37}{4}）}\\{\frac{35}{8}（t=\frac{37}{4}）}\end{array}\right.$
④当5≤t＜8时，如图5，过N作NH⊥AB于H，
由（1）得：EH=$\frac{7}{4}$，
∴S=S_梯形MEFN=$\frac{1}{2}$（MN+EF）•ME=$\frac{1}{2}$（$\frac{7}{4}$+3）×$\frac{5}{2}$=$\frac{95}{16}$；
⑤当8≤t＜$\frac{37}{4}$时，如图6，过M作MN⊥AB于N，
∵PM=$\frac{7}{4}$，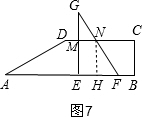
∴PD=$\frac{7}{2}$，
由题意得：BF=AF-AB=3+t-11=8-t，
∴BQ=2BF=2t-16，
∴S=S_△DEF-S_△DPM-S_△BQF，
=$\frac{1}{2}$×3×6-$\frac{1}{2}$×$\frac{7}{4}×\frac{7}{2}$-$\frac{1}{2}$（t-8）（2t-16），
=t²-16t+$\frac{1119}{16}$；
⑥当点C落在线段FG上时，如图7，EF在直线AB上，
由（1）得：BE=$\frac{7}{4}$，
∴t=AB-BE=11-$\frac{7}{4}$=$\frac{37}{4}$，
当t=$\frac{37}{4}$时，S=S_矩形MEBC=BE•BC=$\frac{7}{4}$×$\frac{5}{2}$=$\frac{35}{8}$；
综上所述：S与t的函数关系式为：
S=$\left\{\begin{array}{l}{\frac{9}{5}（t=0）}\\{-\frac{1}{20}{t}^{2}+\frac{6}{5}t+\frac{9}{5}（0＜t≤\frac{13}{4}）}\\{-\frac{1}{4}{t}^{2}+\frac{5t}{2}-\frac{5}{16}（\frac{13}{4}＜t＜5）}\\{\frac{95}{16}（5≤t＜8）}\\{{t}^{2}-16t+\frac{1119}{16}（8≤t＜\frac{37}{4}）}\\{\frac{35}{8}（t=\frac{37}{4}）}\end{array}\right.$
（3）①当AM=MN时，钝角△AMN为等腰三角形，如图8，
∴∠MAN=∠MNA，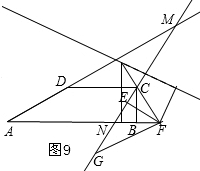
在Rt△FHN中，∵FH=3，
tan∠MNA=tan∠MAN=$\frac{1}{2}$，
∴NH=6，
∴FN=$\sqrt{{6}^{2}+{3}^{2}}$=$\sqrt{45}$=3$\sqrt{5}$，
∴AN=AB+BF+FN=11+$\frac{5}{4}$+3$\sqrt{5}$=$\frac{49+12\sqrt{5}}{4}$；
②当AN=MN时，钝角△AMN为等腰三角形，如图9，
∴∠DAB=∠AMN，
如图2得：tan∠G=$\frac{1}{2}$，tan∠DAB=$\frac{\frac{5}{2}}{5}$=$\frac{1}{2}$，
∴∠G=∠DAB，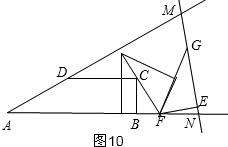
∴∠G=∠AMN，
∴AM∥FG，
∴∠DAB=∠NFG，
∴∠G=∠NFG，
∴GN=FN，
设FN=x，则NG=x，EN=6-x，
在Rt△NEF中，则勾股定理得：3²+（6-x）²=x²，
解得：x=$\frac{15}{4}$，
∴AN=AB+BF-FN=11+$\frac{5}{4}$-$\frac{15}{4}$=$\frac{17}{2}$；
③当AM=AN时，如图10，△AMN不是钝角三角形；
综上所述：当AN=$\frac{49+12\sqrt{5}}{4}$或$\frac{17}{2}$时，△AMN为钝角等腰三角形．

点评 本题是几何变换的综合题，考查了直角梯形、直角三角形的性质，以△EFG运动为主，弄清运动的路径，从△EFG运动的特殊位置入手，正确画出图形，并怀相似和三角函数相结合，表示边的长或求出边的长；对于求重叠部分的面积，也是先分析特殊位置时的重叠部分，再分情况进行讨论，得出结论．