
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:选择题
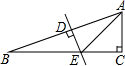 如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=1,则BE的长是( )
如图,在△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=1,则BE的长是( )| A. | 3 | B. | $\sqrt{2}$ | C. | 2 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
国家推行“节能减排,低碳经济”政策后,某环保节能设备生产的产品供不应求,若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于44万元,每套产品的售价不低于80万元.已知这种设备的月产量x(套)与每套的售价y1(万元)间满足关系式y1=160-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
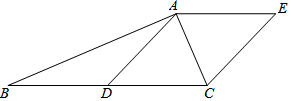 如图,Rt△ABC中,∠BAC=90°,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.
如图,Rt△ABC中,∠BAC=90°,D是BC边的中点,连接AD,过点A作AE∥BC,且AE=CD,连接EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
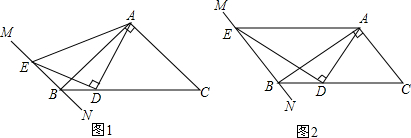
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
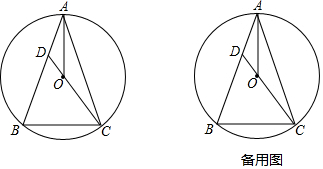
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. | 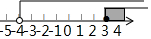 | D. | 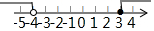 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com