
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:

操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
【答案】操作一(1) 14cm (2) 35° 操作二 CD=4.5
【解析】
试题:操作一利用对称找准相等的量:BD=AD,∠BAD=∠B,然后分别利用周长及三角形的内角和可求得答案;
操作二 利用折叠找着AC=AE,利用勾股定理列式求出AB,设CD=x,表示出BD,AE,在Rt△BDE中,利用勾股定理可得答案;
试题解析:操作一:
(1)由折叠的性质可得AD=BD,∵△ACD的周长=AC+CD+AD,
∴△ACD的周长=AC+CD+BD=AC+BC=8+6=14(cm);
(2)设∠CAD=4x,∠BAD=7x由题意得方程:
7x+7x+4x=90,
解之得x=5,
所以∠B=35°;
操作二:∵AC=9cm,BC=12cm,
∴AB=![]() (cm),
(cm),
根据折叠性质可得AC=AE=9cm,
∴BE=AB-AE=6cm,
设CD=x,则BD=12-x,DE=x,
在Rt△BDE中,由题意可得方程x2+62=(12-x)2,
解之得x=4.5,
∴CD=4.5cm.


科目:初中数学 来源: 题型:
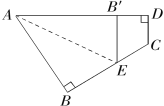
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=![]() ,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;并说明理由.
(2)如果∠C=![]() ,求∠AEB的度数.
,求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角尺叠放如图 1 所示,现将 45°的三角尺ADE 固定不动,将含 30°的三角尺 ABC 绕顶点 A 顺时针转动(旋转角不超过 180 度),使两块三角尺至少有一组边互相平行.如图 2:当∠BAD=15°时,BC∥DE.则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题:
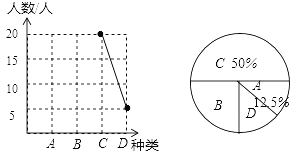
(1)请补全折线统计图,并求出“动漫潮”所在扇形的圆心角度数.
(2)据统计,在被调查的学生中,喜欢“文艺范”类型的仅有2名住读生,其余均为走读生,初二年级欲从喜欢“文艺范”的这几名同学中随机抽取两名同学去观摩“文明礼仪大赛”视频,用列表法或树状图的方法求出所选的两名同学都是走读生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,三角形ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(2,4),点B的坐标为(1,1),点C的坐标为(3,2).
(1)将三角形ABC先沿着x轴负方向平移6个单位,再沿y轴负方向平移2个单位得到三角形A1B1C1,在图中画出三角形A1B1C1;
(2)分别写出A1,B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,其中
,其中![]() 是常数,该抛物线的对称轴为直线
是常数,该抛物线的对称轴为直线![]() .
.
(![]() )求该抛物线的函数解析式.
)求该抛物线的函数解析式.
(![]() )把该抛物线沿
)把该抛物线沿![]() 轴向上平移多少个单位后,得到的抛物线与
轴向上平移多少个单位后,得到的抛物线与![]() 轴只有一个公共点.
轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种进价为![]() 元/个的计算器,其销售量
元/个的计算器,其销售量![]() (万个)与销售价格
(万个)与销售价格![]() (元/个)的变化如下表:
(元/个)的变化如下表:
价格 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
同时,销售过程中的其他开支(不含造价)总计![]() 万元.
万元.
(![]() )观察并分析表中的
)观察并分析表中的![]() 与
与![]() 之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出
之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出![]() (万个)与
(万个)与![]() (元/个)的函数解析式.
(元/个)的函数解析式.
(![]() )求出该公司销售这种计算器的净得利润
)求出该公司销售这种计算器的净得利润![]() (万个)与销售价格
(万个)与销售价格![]() (元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(![]() )该公司要求净得利润不能低于
)该公司要求净得利润不能低于![]() 万元,请写出销售价格
万元,请写出销售价格![]() (元/个)的取值范围.
(元/个)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划最多用41万元购买8台这两种型号的机器人,则该公司该如何购买,才能使得每小时的分拣量最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com