【题目】如图，△ABC与△ADE都是直角三角形，∠C=∠AED=
，点E在AB上，∠D=
.如果△ABC经顺时针旋转后能与△ADE重合，那么旋转中心是点______，旋转了______度
科目：初中数学 来源： 题型：
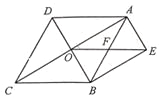
【题目】如图，菱形ABCD的对角线AC、BD相交于点O，BE∥AC，AE∥BD，OE与AB交于点F.
（1）试判断四边形AEBO的形状，并说明理由；
（2）若OE=10，AC=16，求菱形ABCD的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
在平面直角坐标系
中.
（1）请直接写出点
、
两点的坐标：：___________；：___________；
（2）若把向上平移3个单位，再向右平移2个单位得
，请在上图中画出，并写出点
的坐标___________；
（3）求的面积是多少.
查看答案和解析>>
科目：初中数学 来源： 题型：
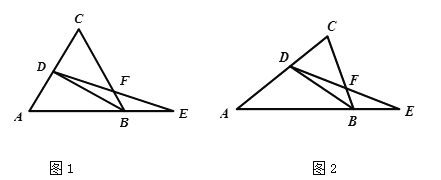
【题目】在△ABC中，AB＝AC，∠ABC的平分线交AC于点D，在AB的延长线上截取BE，使BE＝CD，连接DE交BC于点F．
（1）如图1，当∠CAB＝60°时，若AB＝2，求DE的长度；
（2）如图2，当∠CAB≠60°时，求证：BE＝2BF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明在课外学习时遇到这样一个问题：
定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．
求函数y=﹣x2+4x﹣3的“旋转函数”．小明是这样思考的：由函数y=﹣x2+4x﹣3可知，a1=﹣1，b1=4，c1=﹣3，根据a1+a2=0，b1=b2，c1+c2=0，求出a2，b2，c2，就能确定这个函数的“旋转函数”．
（1）请参考小明的方法写出函数y=﹣x2+4x﹣3的“旋转函数”；
（2）若函数
与y=x2﹣3nx+n互为“旋转函数”，求
．
查看答案和解析>>
科目：初中数学 来源： 题型：
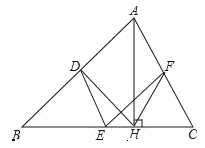
【题目】如图，在△ABC中，点D、E、F分别是边AB、BC、CA的中点，AH是边BC上的高．
（1）求证：四边形ADEF是平行四边形；
（2）若∠AHF＝20°，∠AHD＝50°，求∠DEF的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，长方形ABCD中，AB＝3，BC＝4，点E是BC边上任一点，连接AE，把∠B沿AE折叠，使点B落在点B′处，当CE的长为_____时，△CEB′恰好为直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解学生每周课外阅读时间的情况，对3000名学生采用随机抽样的方式进行了问卷调查，调查结果分为“2小时以内”、“2小时～3小时”、“3小时～4小时”和“4小时以上”四个等级，分别用A、B、C、D表示，根据调查结果绘制成了如图所示的两幅不完整的统计图，由图中所给出的信息解答下列问题：
（1）x＝ ，样本容量是 ；
（2）将不完整的条形统计图补充完整；
（3）请估计该校3000名学生中每周课外阅读时间在“2小时以上”的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并解决后面的问题．
材料：对数的创始人是苏格兰数学家纳皮尔（J．Npler，1550-1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evler，1707-1783）才发现指数与对数之间的联系．我们知道，n个相同的因数a相乘
记为
，如
，此时，3叫做以2为底8的对数，记为
，即
．
一般地，若
（
且
，
），则n叫做以a为底b的对数，记为
，即
．如
，则4叫做以3为底81的对数，记为
，即
．
（1）计算下列各对数的值：
________，
________，
________；
（2）通过观察（1）中三数
、
、
之间满足的关系式是________；
（3）拓展延伸；下面这个一般性的结论成立吗？我们来证明
（且
，
，
）
证明：设
，
，
由对数的定义得：
，
，
∴
，
∴
，
又∵
，
，
∴
（且，，）.
（4）仿照（3）的证明，你能证明下面的一般性结论吗？
（且，，）.
（5）计算：
的值为________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
