
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1) 求一次函数的表达式;
(2) 根据图象写出kx+b-![]() <0的x的取值范围.
<0的x的取值范围.
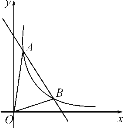
【答案】(1) 一次函数的解析式为y=-2x+8;(2) 0<x<1或x>3
【解析】
(1)先把A、B点坐标代入y=![]() ,求出m、n的值;然后将其分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值即可;
,求出m、n的值;然后将其分别代入一次函数解析式,列出关于系数k、b的方程组,通过解方程组求得它们的值即可;
(2)根据该不等式的解集即为直线在双曲线下方时x的范围即可写出答案;
解:(1)∵点A(m,6),B(3,n)两点在反比例函数![]() (x>0)的图象上,
(x>0)的图象上,
∴6m=3n=6,
∴m=1,n=2,
∴A(1,6),B(3,2).
又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴![]()
解得![]()
则该一次函数的解析式为:y=2x+8;
(2)根据图象可知使![]() 成立的x的取值范围是0<x<1或x>3;
成立的x的取值范围是0<x<1或x>3;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
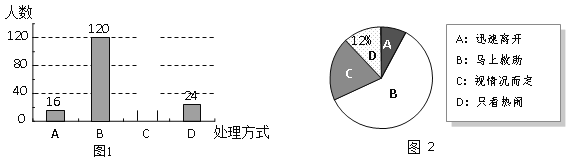
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P,Q两点为同族点.下图中的P,Q两点即为同族点.
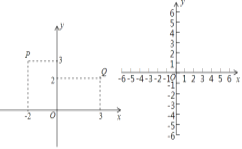
(1)已知点A的坐标为(![]() ,1),
,1),
①在点R(0,4),S(2,2),T(2, ![]() )中,为点A的同族点的是 ;
)中,为点A的同族点的是 ;
②若点B在x轴上,且A,B两点为同族点,则点B的坐标为 ;
(2)直线l: ![]() ,与x轴交于点C,与y轴交于点D,
,与x轴交于点C,与y轴交于点D,
①M为线段CD上一点,若在直线![]() 上存在点N,使得M,N两点为同族点,求n的取值范围;
上存在点N,使得M,N两点为同族点,求n的取值范围;
②M为直线l上的一个动点,若以(m,0)为圆心, ![]() 为半径的圆上存在点N,使得M,N两点为同族点,直接写出m的取值范围.
为半径的圆上存在点N,使得M,N两点为同族点,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为![]() 千米,出租车离甲地的距离为
千米,出租车离甲地的距离为![]() 千米,两车行驶的时间为
千米,两车行驶的时间为![]() 小时,
小时,![]() 、
、![]() 关于
关于![]() 的函数图像如图所示:
的函数图像如图所示:
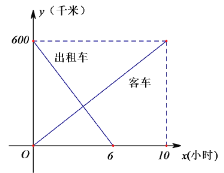
(1)根据图像,求出![]() 、
、![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)设两车之间的距离为![]() 千米.
千米.
①求两车相遇前![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②求出租车到达甲地后![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)甲、乙两地间有![]() 、
、![]() 两个加油站,相距200千米,若客车进入
两个加油站,相距200千米,若客车进入![]() 加油站时,出租车恰好进入
加油站时,出租车恰好进入![]() 加油站,求
加油站,求![]() 加油站离甲地的距离.
加油站离甲地的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
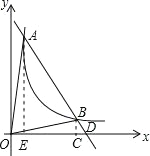
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.
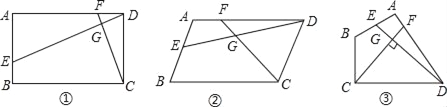
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且ADDF=AEDC,求证:DE⊥CF:
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DECD=CFDA:
(3)如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断![]() 是否为定值,并证明.
是否为定值,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
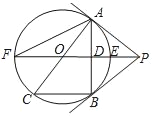
【题目】如图,PB为⊙O的切线,点B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF,
(1)求证:直线PA为⊙O的切线;
(2)若BC=6,tan∠F=![]() ,求cos∠ACB的值.
,求cos∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节假日期间,昀昀一家去公园游玩,在一个场所有一个“守株待兔”的游戏,游戏设计者提供了一只兔子和一个有A、B、C、D四个出入口的兔笼,而且笼内的兔子从每个出入口走出兔笼的机会是均等的.游戏规定:①玩家只能将小兔从A、B两个出入口放入;②如果小兔进入笼子后选择从开始进入的出入口离开,则可获得一只价值4元的小兔玩具,否则应付费3元.
(1)画树状图或列表格,写出该游戏的所有可能结果;
(2)昀昀玩该游戏得到小兔玩具的机会有多大?
(3)假设有120人次玩此游戏,估计游戏设计者可赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
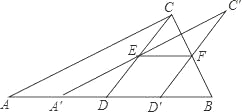
【题目】如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(4分)一元二次方程![]() 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
【答案】A.
【解析】
试题∵△=![]() ,∴方程有两个不相等的实数根.故选A.
,∴方程有两个不相等的实数根.故选A.
考点:根的判别式.
【题型】单选题
【结束】
9
【题目】已知直线y=kx(k>0)与双曲线![]() 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
A.﹣6 B.﹣9 C.0 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com