
分析 (1)根据大于零的分数是正分数,可得正分数集合;
(2)根据大于等于零的数是非负数,可得非负数集合;
(3)整数(像-2,-1,0,1,2这样的数;
(4)根据大于等于零的整数是非负整数,可得非负整数集合;
(5)根据有理数的定义可得有理数集合.
解答 解:(1)正分数集合:{-(-3.14),$\frac{22}{7}$ …};
(2)非负数集合:{ 0,-(-3.14),$\frac{22}{7}$,2003,-(-6)…};
(3)整数集合:{-5,0,2003,-(-6),-|-12|…};
(4)非负整数集合:{ 0,2003,-(-6)…};
(5)有理数集合:{-5,-$\frac{3}{4}$,0,-(-3.14),-2.4,$\frac{22}{7}$,2003,-1.99,-(-6),-|-12|…}.
故答案为:(1){-(-3.14),$\frac{22}{7}$ …};(2){ 0,-(-3.14),$\frac{22}{7}$,2003,-(-6)…};(3){-5,0,2003,-(-6),-|-12|…};(4){ 0,2003,-(-6)…};(5){-5,-$\frac{3}{4}$,0,-(-3.14),-2.4,$\frac{22}{7}$,2003,-1.99,-(-6),-|-12|…}.
点评 本题主要考查的是有理数的定义以及其正分数、非负数、整数和非负整数的定义,比较简单.


科目:初中数学 来源: 题型:解答题
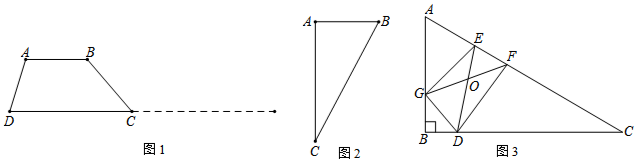
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 3 | … |
| y | … | 0 | 3/2 | 0 | … |
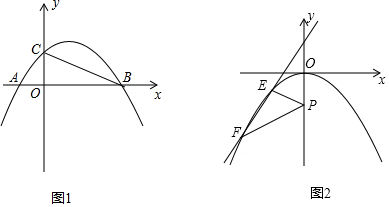
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com