
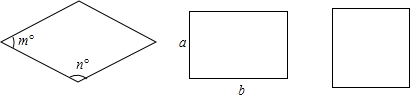
��ͼ�����Ρ������������ε���״�в��죬���ǽ����Ρ������������εĽӽ��̶ȳ�Ϊ���ӽ��ȡ������о����ӽ��ȡ�ʱ��Ӧ��֤����ͼ�εġ��ӽ��ȡ���ȣ�
��1�����������������ڽǵĶ����ֱ�Ϊm���n�㣬�����εġ��ӽ��ȡ�����Ϊ|m��n|������|m��n|ԽС������Խ�ӽ��������Σ�
�������ε�һ���ڽ�Ϊ70�㣬������εġ��ӽ��ȡ�������_________����
�ڵ����εġ��ӽ��ȡ�������_________��ʱ�������������Σ�
��2����������������߳��ֱ���a��b��a��b���������εġ��ӽ��ȡ�����Ϊ|a��b|������|a��b|ԽС������Խ�ӽ��������Σ�
����Ϊ����˵���Ƿ�����������������������εġ��ӽ��ȡ�һ���������壮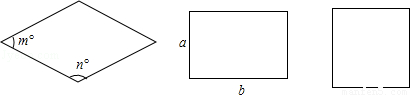
��1����40 ��0 ��2�������������ɼ�����
��������
�����������1����������ͼ�εĶ���֪������ͼ�ε���״��ͬ������С��һ����ͬ������ͼ�εġ��ӽ��ȡ���ȣ����������ε�һ���ڽ�Ϊ70�㣬������εġ��ӽ��ȡ�����|m��n|�������εġ��ӽ��ȡ�����0ʱ�������������Σ�
��2������������������˵����
�⣺��1���١��ڽ�Ϊ70�㣬
�����������ڽǵĶ���Ϊ110�㣮
�����εġ��ӽ��ȡ�=|m��n|=|110��70|=40��
�ڵ����εġ��ӽ��ȡ�����0ʱ�������������Σ�
��2����������
���磬���������ƶ���ȫ�ȵľ�����˵�����ǽӽ������εij̶�����ͬ�ģ���|a��b|ȴ����ȣ�
�������巽����Ψһ��
�綨��Ϊ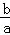 ��
��
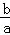 ԽС������Խ�ӽ��������Σ�
ԽС������Խ�ӽ��������Σ�
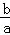 Խ�����������ε���״����Խ��
Խ�����������ε���״����Խ��
�� ʱ�����ξͱ���������Σ�
ʱ�����ξͱ���������Σ�
���㣺����ͼ�Σ����ε����ʣ������ε����ʣ�
��������ȷ���⡰�ӽ��ȡ�����˼�����εġ��ӽ��ȡ�|a��b|ԽС������Խ�ӽ��������Σ����ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 15����ͼ�����Σ������������ε���״�в��죬���ǽ����Ρ������������εĽӽ��̶ȳ�Ϊ���ӽ��ȡ������о����ӽ��ȡ�ʱ��Ӧ��֤����ͼ�εġ��ӽ��ȡ���ȣ����������������ڽǵĶ����ֱ�Ϊm���n�㣬�����εġ��ӽ��ȡ�����Ϊ|m-n|�����ǣ�|m-n|ԽС������Խ�ӽ��������Σ�
15����ͼ�����Σ������������ε���״�в��죬���ǽ����Ρ������������εĽӽ��̶ȳ�Ϊ���ӽ��ȡ������о����ӽ��ȡ�ʱ��Ӧ��֤����ͼ�εġ��ӽ��ȡ���ȣ����������������ڽǵĶ����ֱ�Ϊm���n�㣬�����εġ��ӽ��ȡ�����Ϊ|m-n|�����ǣ�|m-n|ԽС������Խ�ӽ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2007����б�ҵ��ѧ���ԣ����ճ��ݾ�����ѧ���������� ���ͣ������
��ͼ�����Ρ������������ε���״�в��죬���ǽ����Ρ������������εĽӽ��̶ȳ�Ϊ���ӽ��ȡ������о����ӽ��ȡ�ʱ��Ӧ��֤����ͼ�εġ��ӽ��ȡ���ȣ�
��1�����������������ڽǵĶ����ֱ�Ϊ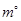 ��
��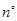 �������εġ��ӽ��ȡ�����Ϊ
�������εġ��ӽ��ȡ�����Ϊ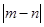 �����ǣ�
�����ǣ�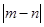 ԽС������Խ�ӽ��������Σ�
ԽС������Խ�ӽ��������Σ�
�������ε�һ���ڽ�Ϊ ��������εġ��ӽ��ȡ����� ��
��������εġ��ӽ��ȡ����� ��
�ڵ����εġ��ӽ��ȡ����� ʱ�������������Σ�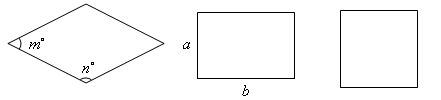
��2����������������߳��ֱ���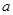 ��
��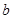 ��
�� ���������εġ��ӽ��ȡ�����Ϊ
���������εġ��ӽ��ȡ�����Ϊ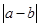 ������
������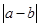 ԽС������Խ�ӽ��������Σ�
ԽС������Խ�ӽ��������Σ�
����Ϊ����˵���Ƿ�����������������������εġ��ӽ��ȡ�һ���������壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013�������ѧ��Ԫ���Ų��Ծ�-����ͼ�Σ������棩 ���ͣ������
��ͼ�����Σ������������ε���״�в��죬���ǽ����Ρ������������εĽӽ��̶ȳ�Ϊ���ӽ��ȡ������о����ӽ��ȡ�ʱ��Ӧ��֤����ͼ�εġ��ӽ��ȡ���ȣ����������������ڽǵĶ����ֱ�Ϊm���n�㣬�����εġ��ӽ��ȡ�����Ϊ|m��n|�����ǣ�|m��n|ԽС������Խ�ӽ��������Σ�
�������ε�һ���ڽ�Ϊ70�㣬������εġ��ӽ��ȡ�������_________����
�ڵ����εġ��ӽ��ȡ�������_________��ʱ�������������Σ�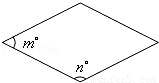
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com