
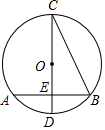
 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=4$\sqrt{2}$,∠BCD=30°,则⊙O的半径为$\frac{4\sqrt{6}}{3}$.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=4$\sqrt{2}$,∠BCD=30°,则⊙O的半径为$\frac{4\sqrt{6}}{3}$. 分析 首先连接OB,由在⊙O中,CD是直径,弦AB⊥CD,根据垂径定理的即可求得BE的长,由圆周角定理可求得∠BOE的度数,然后利用三角函数,求得答案.
解答 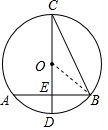 解:连接OB,
解:连接OB,
∵在⊙O中,CD是直径,弦AB⊥CD,
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{2}$=2$\sqrt{2}$,
∵∠BOD=2∠BCD=2×30°=60°,
∴OB=$\frac{BE}{sin60°}$=$\frac{4\sqrt{6}}{3}$,
即⊙O的半径为:$\frac{4\sqrt{6}}{3}$.
故答案为:$\frac{4\sqrt{6}}{3}$.
点评 此题考查了圆周角定理、垂径定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在一次自行车越野赛中,出发mh后,小明骑行了25km,小刚骑行了18km,此后两人分别以a km/h,b km/h匀速骑行,他们骑行的时间t(单位:h)与骑行的路程s(单位:km)之间的函数关系如图所示,观察图象,下列说法:
在一次自行车越野赛中,出发mh后,小明骑行了25km,小刚骑行了18km,此后两人分别以a km/h,b km/h匀速骑行,他们骑行的时间t(单位:h)与骑行的路程s(单位:km)之间的函数关系如图所示,观察图象,下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com