
【题目】如图,已知数轴上有两点![]() ,它们的对应数分别是
,它们的对应数分别是![]() ,其中
,其中![]()
![]()
(1)在![]() 左侧作线段
左侧作线段![]() ,在
,在![]() 的右侧作线段
的右侧作线段![]() (要求尺规作图,不写作法,保留作图痕迹)
(要求尺规作图,不写作法,保留作图痕迹)
(2)若点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() ,且
,且![]() ,求
,求![]() 的值
的值
(3)在(2)的条件下,设点![]() 是
是![]() 的中点,
的中点,![]() 是数轴上一点,且
是数轴上一点,且![]() ,请直接写出
,请直接写出![]() 的长
的长
【答案】(1)见解析;(2)c=-68;d=92;(3)28或![]()
【解析】
(1)首先画射线,在射线上截取AC=AB,再在射线BA上截取BD=3AB;
(2)由题意可得AC=80,AD=80,据此解答即可;
(3)分情况讨论:①点N在线段CD上;②点N在线段CD的延长线上分别进行解答即可.
(1)解:如图,线段![]() 为所求的线段
为所求的线段

(2)因为![]()
![]()
![]() ;
;
(3)分情况讨论:
①点N在线段CD上,
由(2)得CD=92(68)=160,点B对应的数为1240=28,
![]()
∴BD=92(28)=120,
∵点M是BD的中点,
∴点M对应的数为9260=32,
∵CN=4DN,
∴DN=![]() CD=32,
CD=32,
∴点N对应的数为9232=60,
∴MN=6032=28;
②点N在线段CD的延长线上,
∵CN=4DN,
∴DN=![]() CD=
CD=![]() ,
,
∴点N对应的数为92+![]() =
=![]() ,
,
∴MN=![]() 32=
32=![]() .
.
故![]() 的长为28或
的长为28或![]() .
.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解一批灯泡的使用寿命,宜采用普查方式
B.掷两枚质地均匀的硬币,两枚硬币都是正面朝上这一事件发生的概率为![]()
C.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
D.甲乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
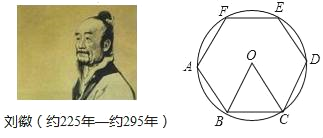
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:过直线外一点作已知直线的垂线,已知:如图(1),直线![]() 及外一点
及外一点![]() ,求作
,求作![]() 的垂线,使它经过点
的垂线,使它经过点![]() ,小红的做法如下:
,小红的做法如下:
①在直线![]() 上任取一点B,连接
上任取一点B,连接![]()
②以![]() 为圆心,
为圆心,![]() 长为半径作弧,交直线
长为半径作弧,交直线![]() 于点
于点![]() ;
;
③分别以![]() 为圆心,
为圆心, ![]() 长为半径作弧,两弧相交于点
长为半径作弧,两弧相交于点![]() ;
;
④作直线![]() ,直线
,直线![]() 即为所求如图(2),小红的做题依据是( )
即为所求如图(2),小红的做题依据是( )
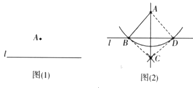
A.四条边都相等的四边形是菱形;菱形的对角线互相垂直
B.直径所对的圆周角是直角
C.直线外一点到这条直线上垂线段最短
D.同圆或等圆中半径相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月26日11:30,全球新冠肺炎确诊病例突破47万例,已有60个国家宣布进入紧急状态,国外较多医护人员不得不重复使用一次性口罩和防护装备.深圳海王星辰福田某药店购进A、B两种一次性口罩共1500个,已知购进A种一次性口罩和B种一次性口罩的费用分别为3000元和2000元,且A种一次性口罩的单价比B种一次性口罩单价多1元,求A、B两种一次性口罩的单价各是多少?设A种一次性口罩单价为x元,根据题意,列方程正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据如图9给出的数轴,解答下面的问题:
![]()
(1)请你根据图中![]() 两点的位置,分别写出它们所表示的有理数
两点的位置,分别写出它们所表示的有理数![]() _____ ;
_____ ;![]()
(2)观察数轴,与点![]() 的距离为
的距离为![]() 的点表示的数是:
的点表示的数是:
(3)若将数轴折叠,使得![]() 与
与![]() 表示的点重合,则
表示的点重合,则![]() 点与数 表示的点重合;
点与数 表示的点重合;
(4)若数轴上![]() 两点之间的距离为
两点之间的距离为![]() (
(![]() 在
在![]() 的左侧),且
的左侧),且![]() 两点经过(3)中折叠后互重合,则
两点经过(3)中折叠后互重合,则![]() 两点表示的数分别是:
两点表示的数分别是:![]() ;
;![]() :
:
(5)若数轴上![]() 两点之间的距离为
两点之间的距离为![]() (
(![]() 在
在![]() 的左侧,且
的左侧,且![]() 两点经过
两点经过![]() 中折叠后互重合,则
中折叠后互重合,则![]() 两点表示的数分别是:
两点表示的数分别是:![]() ;
;![]() :
:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一动点,连结
上一动点,连结![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() .
.
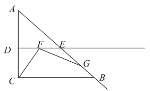
(1)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 与
与![]() 的大小关系;
的大小关系;
(2)当![]() 等于多少时,
等于多少时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com