
【题目】已知数轴上两点![]() 、
、![]() ,其中A表示的数为-2,
,其中A表示的数为-2,![]() 表示的数为2,若在数轴上存在一点
表示的数为2,若在数轴上存在一点![]() ,使得
,使得![]() ,则称点
,则称点![]() 叫做点
叫做点![]() 、
、![]() 的“
的“![]() 节点”,例如图1所示,若点
节点”,例如图1所示,若点![]() 表示的数为0,有
表示的数为0,有![]() ,则称点
,则称点![]() 为点
为点![]() 、
、![]() 的“4节点”.
的“4节点”.

请根据上述规定回答下列问题:
(1)若点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,且点
节点”,且点![]() 在数轴上表示的数为-4,求
在数轴上表示的数为-4,求![]() 的值.
的值.
(2)若点![]() 是数轴上点
是数轴上点![]() 、
、![]() 的“5节点”,请你直接写出点
的“5节点”,请你直接写出点![]() 表示的数为____________;
表示的数为____________;
(3)若点![]() 在数轴上(不与
在数轴上(不与![]() 、
、![]() 重合),满足
重合),满足![]() 、
、![]() 之间的距离是
之间的距离是![]() 、
、![]() 之间距离的一半,且此时点
之间距离的一半,且此时点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,求
节点”,求![]() 的值.
的值.
【答案】(1)8;(2)![]() ;(3)4或12
;(3)4或12
【解析】
(1)利用"n节点"的概念进行解答即可;
(2)设点D表示的数为x,由"5节点"的定义列出方程分情况进行解答;
(3)根据点E的不同位置:①当点E在BA延长线上时;②当点E在线段AB上时;③当点E在AB延长线上时,根据BE=![]() AE,先求点E表示的数,再根据AC+BC=n,列方程解答即可.
AE,先求点E表示的数,再根据AC+BC=n,列方程解答即可.
解:(1)由A表示的数为-2,B表示的数为2,点C在数轴上表示的数为-4,
∴AC=2,BC=6,
∴n=AC+BC-2+6=8.
(2)如图:

∵点D是数轴上点A、B的“5节点"
∴AC+BC=5,
∵AB=4
∴C在点A的左侧或在点A的右侧,
设点D表示的数为x,则AC+BC=5,
∴-2-x+2-x=5或x-2+x-(-2)=5,x=-2.5或2.5,
则点D表示的数为2.5或-2.5;
(3) 根据点E和BE的位置关系,需分三种情况:
①当点E在BA延长线上时,BE不可能等于![]() AE,故舍弃;
AE,故舍弃;
②当点E在线段AB上时,满足BE=![]() AE,如图:
AE,如图:

∴n=AE+BE=AB=4;
③当点E在AB延长线上时,如图:
![]()
∵BE=![]() AE
AE
∴BE=AB=4,
∴点E表示的数为6,
则n=AE+BE=8+4=12
所以 n=4或n=12.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
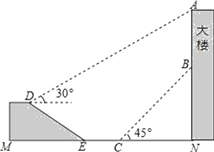
【题目】如图,钟鼓楼AN上悬挂一条幅AB,谢高在坡面D处测得条幅顶部A的仰角为30°,沿坡面向下走到坡脚E处,然后向钟鼓楼方向继续行走10米来到C处,测得条幅的底部B的仰角为45°,此时谢高距钟鼓楼底端N处20米.已知坡面DE=20米,山坡的坡度i=1:![]() (即tan∠DEM=1:
(即tan∠DEM=1:![]() ),且M、E、C、N在同一条直线上,求条幅的长度(结果精确到1米)
),且M、E、C、N在同一条直线上,求条幅的长度(结果精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)30-(-12)-(-25)-18+(-10)
(2) (-![]() +
+![]() -
-![]() )
)![]()
![]() .
.
(3)-52÷(-3)2×(-5)3÷[-(-5)2]
(4)(-2![]() +3
+3![]() )-(2
)-(2![]() -
-![]() )+6
)+6![]()
(5)![]()
![]() -[
-[![]() (
(![]() -
-![]() )+4
)+4![]() ]-
]-![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.
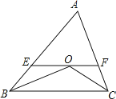
(1) 结合图形,请你写出你认为正确的结论;
(2) 过O作EF∥BC交AB于E,交AC于F. 请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系;

(3) 若AB≠AC,其他条件不变,图中还有等腰三角形吗?若有,请写出所有的等腰三角形,若没有,请说明理由;线段EF、BE、FC之间,上面探究的结论是否还成立?
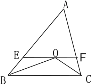
查看答案和解析>>
科目:初中数学 来源: 题型:
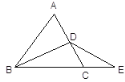
【题目】已知:如图,BD是等边△ABC一边上的高,延长BC至E,使CE=CD.
(1)试比较BD与DE的大小关系,并说明理由;
(2)若将BD改为△ABC的角平分线或中线,能否得出同样的结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,∠ACB=90°,∠BAC=30°,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
(1)当点B于点O重合的时候,求三角板运动的时间;
(2)三角板继续向右运动,当B点和E点重合时,AC与半圆相切于点F,连接EF,如图2所示.
①求证:EF平分∠AEC;
②求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,直线a经过点A,且BE⊥a于E,DF⊥a于F.
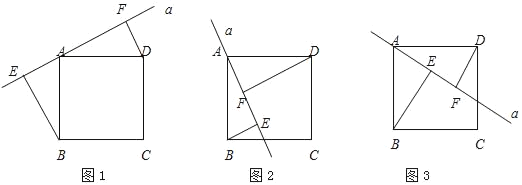
(1)当直线a绕点A旋转到图1的位置时,求证:①△ABE≌△DAF;②EF=BE+DF;
(2)当直线a绕点A旋转到图2的位置时,试探究EF、BE、DF具有怎样的等量关系?请写出这个等量关系,并加以证明;
(3)当直线a绕点A旋转到图3的位置时,试问DF、EF、BE具有怎样的等量关系?请写出这个等量关系,不证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com