
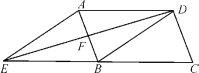
【题目】如图,在平行四边形ABCD中,DB=DA,∠ADB的平分线交AB于点F,交CB的延长线于点E,连接AE.
(1)求证:四边形AEBD是菱形;
(2)若DC=![]() ,EF:BF=3,求菱形AEBD的面积.
,EF:BF=3,求菱形AEBD的面积.
【答案】(1)见解析;(2)15.
【解析】
(1)由△AFD≌△BFE,推出AD=BE,可知四边形AEBD是平行四边形,再根据DB=DA可得结论;
(2)先求出BF的长,再求出EF的长即可解决问题.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥CE,
∴∠DAF=∠EBF,
∵∠AFD=∠EFB,AF=FB,
∴△AFD≌△BFE,
∴AD=EB,∵AD∥EB,
∴四边形AEBD是平行四边形,
∵BD=AD,
∴四边形AEBD是菱形.
(2)∵四边形ABCD是平行四边形,
∴CD=AB=![]() ,
,
∵四边形AEBD是菱形,
∴AB⊥DE,AF=FB=![]() ,
,
∵EF:BF=3
∴EF=![]()
∴DE=2EF=![]()
∴S菱形AEBD=![]() ABDE=
ABDE=![]() ×
×![]() ×3
×3![]() =15.
=15.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4,AD=9点F是边BC上的一点,点E是AD上的一点,AE:ED=1:2,连接EF、DF,若EF=2![]() ,则CF的长为______________。
,则CF的长为______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.
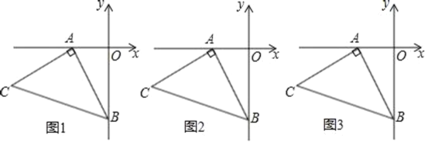
(1)求C点的坐标;
(2)如图1,在平面内是否存在一点H,使得以A、C、B、H为顶点的四边形为平行四边形?若存在,请直接写出H点坐标;若不存在,请说明理由;
(3)如图1点M(1,﹣1)是第四象限内的一点,在y轴上是否存在一点F,使得|FM﹣FC|的值最大?若存在,请求出F点坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年周杰伦地表最强巡回演唱会于11月17日在贵阳奥林匹克体育中心举行,小颖购买了一张票价为四位数的场地票(动感地带专属),而小明一张购买了票价为三位数的看台票(动感地带专属)。小颖说,“在你的票价前面多写个1,都还比我的便宜200元”;小明说,“只需在我的票价后多写个0,就比你的贵3120元”.请问小颖和小明购买的演唱会门票各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
(1)以x(单位:元)表示商品原价,y(单位:元)表示购物金额,分别就两家商场的让利方式写出y关于x的函数解析式;
(2)在同一直角坐标系中画出(1)中函数的图象;
(3)春节期间如何选择这两家商场去购物更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A、B分别是x轴上位于原点左右两侧的点,点P在第一象限,且它的纵坐标为3,直线AP交y轴于点C(0,2),直线PB交y轴于点D,且ΔAOP的面积为6.

(1)求直线AP的关系式;
(2)若ΔBOP与ΔAOP的面积相等,求ΔBOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:
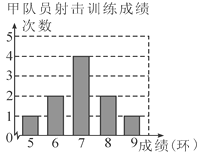

根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com