
【题目】如图,在平面直角坐标系xoy中,A(-1,5)、B(-1,0),C(-4,3).

(1)△ABC的面积是 .
(2)在下图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.
(3)写出点A1、B1、C1的坐标.
科目:初中数学 来源: 题型:
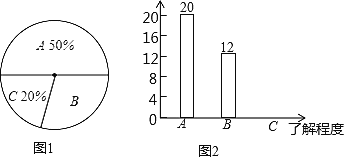
【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉;B:了解较多;C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
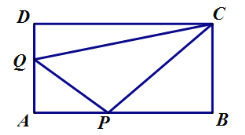
【题目】已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF

(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 秒的速度移动;点
秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以
以![]() 秒的速度移动,如果
秒的速度移动,如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间(
(秒)表示移动的时间(![]() ).
).
(1)当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
(2)求当移动到![]() 为等腰直角三角形时斜边
为等腰直角三角形时斜边![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
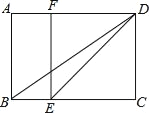
【题目】已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD.
(1)求证:四边形EFCD是正方形;
(2)若BE=1,ED=2![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,对角线AC、BD交于点O,经过点O的直线AD于点E,交BC于点F.
(1)求证:OE=OF;
(2)如图2,连接AF、CE,当AF⊥FC时,在不添加辅助线的情况下,直接写出等于![]() 的线段.
的线段.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com