
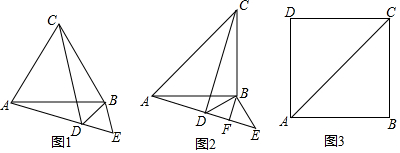
分析 (1)由条件易证△BCD≌△BAE,从而得到:CD=AE,∠BDC=∠BEA.求出∠CDB=60°;
(2)仿照(1)中的解法可求出∠CDB的度数,证出CD=AE;BF是△DBE均为等腰直角三角形,得出CD=AE=AD+DE=AD+2BF.
(3)先判断出△PBE是等腰直角三角形,借助(2)结论得到由(2)的结论可得,CE=AE+2BH,求出BH即可.
解答 解:(1)①∵△ACB和△DBE均为等边三角形,
∴BA=CB,BD=BE,∠ABC=∠DBE=60°.
∴∠ABE=∠CBD.
在△BCD和△BAE中,
∵AB=BC,∠ABE=∠CBD,BD=BE,
∴△BCD≌△BAE(SAS),
∴∠CDB=∠BEA.
∵△DBE为等边三角形,
∴∠CDB=∠BED=60°.
故答案为:60°.
②∵△BCD≌△BAE,
∴CD=AE,
故答案为:CD=AE,
(2))∠CDB=45°,CD=AD+2BF
理由:∵△ACB和△DBE均为等腰直角三角形,
∴BA=CB,BD=BE,∠ABC=∠DBE=90°.
∴∠ABE=∠CBD.
在△BCD和△BAE中,
∵AB=BC,∠ABE=∠CBD,BD=BE,
∴△BCD≌△BAE(SAS),
∴∠CDB=∠AEB,CD=AE
∵BF是△DBE均为等腰直角三角形,
∴∠CDB=∠AEB=45,DE=2BF,
∴CD=AE=AD+DE=AD+2BF.
∴∠CDB=45°,CD=AD+2BF;
(3)①如图,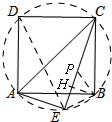
连接EB,ED,作BH⊥CE,BP⊥BE,
∵四边形ABCD是正方形,
∴∠BAC=45°,AB=AD=CD=BC=2,∠ABC=90°,
∴CD=2,
∴AC=2$\sqrt{2}$,
∵AE=1,
∴CE=$\sqrt{7}$,
∵A,E,B,C四点共圆,
∴∠BCE=∠CAB=45°,
∴△PBE是等腰直角三角形,
∵△ABC是等腰直角三角形,且C,E,P共线,BH⊥CE,
∴由(2)的结论可得,CE=AE+2BH,
∴$\sqrt{7}$=2BH+1,
∴BH=$\frac{\sqrt{7}-1}{2}$.
②同①的方法可得,CE=2BH-AE,
∴$\sqrt{7}$=2BH-1,
∴BH=$\frac{\sqrt{7}+1}{2}$,
∴点B到CE的距离为$\frac{\sqrt{7}-1}{2}$或$\frac{\sqrt{7}+1}{2}$.
点评 此题是四边形综合题,主要考查了等边三角形的性质,等腰直角三角形的性质和判定,全等三角形的性质和判定,解本题的关键是全等三角形的判定.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
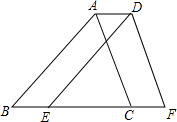 如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )| A. | 2:1 | B. | 3:2 | C. | 4:3 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
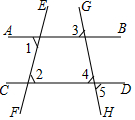 如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.
如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com