
【题目】阅读下列解题过程:已知![]() 、
、![]() 、
、![]() 为△ABC的三边,且满足
为△ABC的三边,且满足![]() ,
,
试判断△ABC的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴△ABC为直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号________;
(2)错误的原因是____________________________;
(3)本题的正确结论是_________________________.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投出多少个3分球?共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
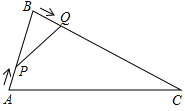
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 是等边
是等边![]() 内的任一点,连接
内的任一点,连接![]() ,
,![]() ,
,![]() .
.
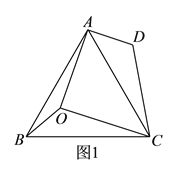
如图![]() ,已知
,已知![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,使
,使![]() 与
与![]() 重合,得
重合,得![]() .
.
(![]() )
)![]() 的度数是__________.
的度数是__________.
(![]() )用等式表示线段
)用等式表示线段![]() ,
,![]() ,
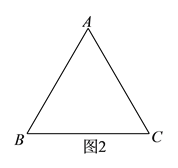
,![]() 之间的数量关系,并证明.(图
之间的数量关系,并证明.(图![]() 为备用图)
为备用图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1 ,以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2 ,再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3 ,…,依次进行下去,则点B6的坐标是( )

A. (﹣8,0) B. (0,﹣8) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在3×3的正方形网格(每个小正方形的边长均为1)中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴(水平线为横轴),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称.

(1)原点是 (填字母A,B,C,D );
(2)若点P在3×3的正方形网格内的坐标轴上,且与四个格点A,B,C,D,中的两点能构成面积为1的等腰直角三角形,则点P的坐标为 (写出可能的所有点P的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
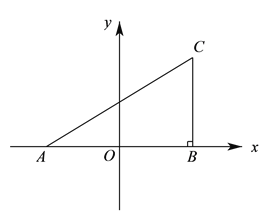
【题目】如图①,在平面直角坐标系中, ![]() ,
, ![]() ,且满足
,且满足![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .
.
(![]() )求
)求![]() 的面积.
的面积.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 和
和![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
(![]() )动点
)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿射线
的速度沿射线![]() 运动,如果在运动过程中
运动,如果在运动过程中![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 运动的时间.
运动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
(1)旋转中心;
(2)旋转角度数;
(3)图中经过旋转后能重合的三角形共有几对?若A、O、C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度;
(5)若∠A=15°,则求当A、C、B在同一条线上时的旋转角度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com