Question

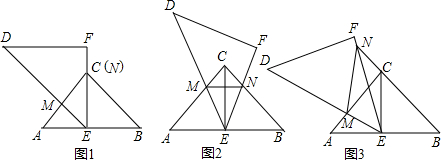
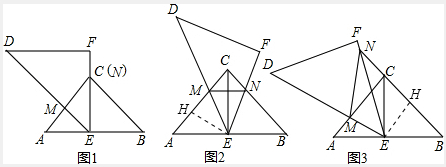
已知两个全等的等腰直角△ABC、△DEF，其中∠ACB=∠DFE=90°，E为AB中点，△DEF可绕顶点E旋转，线段DE，EF分别交线段CA，CB（或它们所在直线）于M、N．
（1）如图l，当线段EF经过△ABC的顶点C时，点N与点C重合，线段DE交AC于M，求证：AM=MC；
（2）如图2，当线段EF与线段BC边交于N点，线段DE与线段AC交于M点，连MN，EC，请探究AM，MN，CN之间的等量关系，并说明理由；
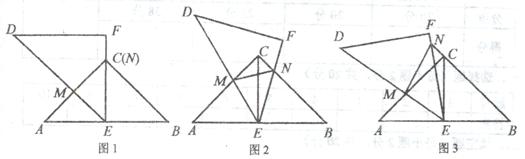
（3）如图3，当线段EF与BC延长线交于N点，线段DE与线段AC交于M点，连MN，EC，请猜想AM，MN，CN之间的等量关系，不必说明理由．

Answer 1

分析：（1）根据AC=BC，E为AB中点，得出CE⊥AB，∠ACE=∠BCE=

1

2

ACB=45°，∠AEC=90°，∠A=∠ACE=45°，AE=CE，再根据DF=EF，∠DFE=90°，得出∠FED=45°，∠FED=

1

2

∠AEC，即可得出AM=MC；                                   
（2）先在AM截取AH，使得AH=CN，连接BH，根据AE=CE，∠A=∠BCE=45°证出△AHE≌△CNE，HE=NE，∠AEH=∠CEN，∠HEM=∠AEC-∠AEH-MEC=∠AEC-∠CEN-MEC=∠AEC-∠MEF=90°-45°=45°，∠HEM=∠NEM=45°然后证出△HEM≌△NEM，HM=MN，最后根据AM=AH+HM=CN+MN即可得出答案；                                
（3）先在CB上截取CH=AM，根据SAS证得△AEM≌△CEH，得出EM=EH，∠AEM=∠CEH，AM=CH，再根据∠MEN和∠AEC的度数，得出∠CEH+∠CEN=∠HEN=45°，再在△EMN和△EHN中，根据SAS证得△EMN≌△EHN，得出MN=HN，即可求出答案．

解答：解：（1）∵AC=BC，E为AB中点，
∴CE⊥AB，∠ACE=∠BCE=

1

2

ACB=45°，
∴∠AEC=90°，
∴∠A=∠ACE=45°，
∴AE=CE，
∵DF=EF，∠DFE=90°，
∴∠FED=45°，
∴∠FED=

1

2

∠AEC，
又∵AE=CE，
∴AM=MC；                                   

（2）AM=MN+CN，理由如下：
在AM截取AH，使得AH=CN，连接BH，
由（1）知AE=CE，∠A=∠BCE=45°
∵在△AHE与△CNE中：

AH=CN ∠A=∠NCE AE=CE

，
∴△AHE≌△CNE（SAS），
∴HE=NE，∠AEH=∠CEN，
∴∠HEM=∠AEC-∠AEH-MEC=∠AEC-∠CEN-MEC=∠AEC-∠MEF=90°-45°=45°，
∴∠HEM=∠NEM=45
∵在△HEM与△NEM中：

EH=EN ∠HEM=∠MEN ME=ME

，
∴△HEM≌△NEM（SAS），
∴HM=MN，
∴AM=AH+HM=CN+MN；
即AM=MN+CN                                

（3）猜得：MN=AM+CN，理由如下：
在CB上截取CH=AM，
在△AEM和△CEH中，

AM=CH ∠A=∠BCE AE=CE

，
∴△AEM≌△CEH（SAS），
∴EM=EH，∠AEM=∠CEH，AM=CH，
∵∠MEN=45°，∠AEC=90°，
∴∠AEM+∠CEN=45°，
∴∠CEH+∠CEN=∠HEN=45°，
∵∠MEN=∠HEN，
在△EMN和△EHN中，

EM=EH ∠MEN=∠HEN EN=EN

，
∴△EMN≌△EHN（SAS），
∴MN=HN，
∴MN=CH+CN，
∴MN=AM+CN．

点评：此题考查了全等三角形的判定与性质，用到的知识点是全等三角形的判定与性质、等腰直角三角形的性质，关键是做出辅助线，构造全等三角形．